题目内容
6.若关于x的方程(k+1)x2-2kx+k-5=0有两个实数根,则k的取值范围k≥-$\frac{5}{4}$且k≠-1.分析 根据x的方程(k+1)x2-2kx+k-5=0有两个实数根得到k+1≠0,△=b2-4ac≥0,列出k的不等式,求出k的取值范围即可.
解答 解:根据题意,可得△=(-2k)2-4×(k+1)×(k-5)≥0,且k+1≠0,
即16k+20≥0且k≠-1,
解得:k≥-$\frac{5}{4}$且k≠-1,
故答案为:k≥-$\frac{5}{4}$且k≠-1.
点评 此题考查了根的判别式,一元二次方程根的情况与判别式△的关系:(1)△>0?方程有两个不相等的实数根;(2)△=0?方程有两个相等的实数;(3)△<0?方程没有实数根.

练习册系列答案
 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
15.市场上猪肉的价格是9.6元/斤,很不好计算金额,但某销售员总能脱口说出金额,原来他记住了下列的表格:
(1)此题中的两个变量分别是x和y,其中自变量是x,因变量是y,y是x的函数.
(2)这是用哪种方法表示的函数?
(3)你能写出y与x之间的关系式吗?
| 斤数x | 1.1 | 1.2 | 1.3 | 1.4 |
| 金额y | 10.56 | 11.52 | 12.48 | 13.44 |
(2)这是用哪种方法表示的函数?
(3)你能写出y与x之间的关系式吗?
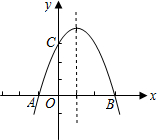 如图所示的抛物线是由抛物线y=-x2向上平移4个单位长度,再向右平移1个单位长度得到,与y轴交于C点.
如图所示的抛物线是由抛物线y=-x2向上平移4个单位长度,再向右平移1个单位长度得到,与y轴交于C点. 画出旋转后的图形:如图,将点线段AB绕点O旋转,使A点的对应点为点A′.
画出旋转后的图形:如图,将点线段AB绕点O旋转,使A点的对应点为点A′.