题目内容
 如图,在?ABCD中,E,F是对角线BD上的两点,连接AE,EC,CF,AF,若四边形AECF为平行四边形,则BE=DF,请说明理由.
如图,在?ABCD中,E,F是对角线BD上的两点,连接AE,EC,CF,AF,若四边形AECF为平行四边形,则BE=DF,请说明理由.考点:平行四边形的性质
专题:
分析:连接AC,交BD于点O,由四边形ABCD、AECF是平行四边形,根据平行四边形的对角线互相平分,即可得OB=OD,OE=OF,继而求得BE=DF.
解答: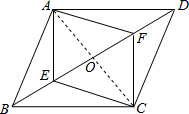 证明:连接AC,交BD于点O,
证明:连接AC,交BD于点O,
∵四边形ABCD、AECF是平行四边形,
∴OB=OD,OE=OF,
∴OB-OE=OD-OF,
即BE=DF.
 证明:连接AC,交BD于点O,
证明:连接AC,交BD于点O,∵四边形ABCD、AECF是平行四边形,
∴OB=OD,OE=OF,
∴OB-OE=OD-OF,
即BE=DF.
点评:此题考查了平行四边形的性质,此题难度适中,注意掌握辅助线的作法,注意数形结合思想的应用.

练习册系列答案
相关题目
下列说法正确的是( )
| A、0.720有两个有效数字 |
| B、3.6万精确到十分位 |
| C、3.5×106精确到十分位 |
| D、5.078精确到0.001 |
| 1 |
| 2 |
| A、3 | ||
B、
| ||
| C、k | ||
| D、k |
若x2-mx-15=(x+3)(x+n),则m、n的值分别为( )
| A、m=-2,n=5 |
| B、m=2,n=-5 |
| C、m=2,n=5 |
| D、m=-2,n=-5 |
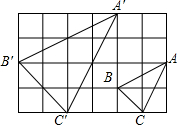 如图,由24个边长为1的正方形组成4×6的网格,若△A′B′C′∽△ABC(相似比不是1),且△A′B′C′,△ABC的顶点都是网格内正方形的顶点,则△A′B′C′的面积是
如图,由24个边长为1的正方形组成4×6的网格,若△A′B′C′∽△ABC(相似比不是1),且△A′B′C′,△ABC的顶点都是网格内正方形的顶点,则△A′B′C′的面积是