题目内容
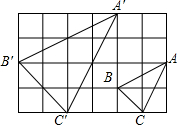 如图,由24个边长为1的正方形组成4×6的网格,若△A′B′C′∽△ABC(相似比不是1),且△A′B′C′,△ABC的顶点都是网格内正方形的顶点,则△A′B′C′的面积是
如图,由24个边长为1的正方形组成4×6的网格,若△A′B′C′∽△ABC(相似比不是1),且△A′B′C′,△ABC的顶点都是网格内正方形的顶点,则△A′B′C′的面积是考点:相似三角形的性质
专题:网格型
分析:易求△ABC的面积,因为△A′B′C′∽△ABC(相似比不是1),利用相似三角形的性质:面积比等于相似比的平方即可求出△A′B′C′的面积.
解答:解:∵△A′B′C′∽△ABC,
∴BC:B′C′=1:2
∵S△ABC=2×2-2×
×2×1-
×1×1=1.5,
∴△A′B′C′=4×1.5=6,
故答案为:6.
∴BC:B′C′=1:2
∵S△ABC=2×2-2×
| 1 |
| 2 |
| 1 |
| 2 |
∴△A′B′C′=4×1.5=6,
故答案为:6.
点评:本题考查对相似三角形性质的理解,相似三角形边长的比等于相似比面积比等于相似比的平方.解答此题的关键是找出相似三角形的对应边.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
下列变形正确的有( )
| A、由x-5=4x+2,可得x-4x=5+2 |
| B、由7x=4x-3,可得7x-4x=3 |
| C、由10x=11x-2,可得10x+11x=-2 |
| D、由5+x=12,可得x=12+5. |
若x3=-27a6b9,则x等于( )
| A、-9a3b6 |
| B、-6a3b6 |
| C、-3a2b6 |
| D、-3a2b3 |
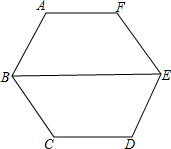 如图,∠A=∠ABC=∠C=120°,且BE平分∠ABC,你能得到AF∥CD吗?请说明理由.
如图,∠A=∠ABC=∠C=120°,且BE平分∠ABC,你能得到AF∥CD吗?请说明理由. 如图,在?ABCD中,E,F是对角线BD上的两点,连接AE,EC,CF,AF,若四边形AECF为平行四边形,则BE=DF,请说明理由.
如图,在?ABCD中,E,F是对角线BD上的两点,连接AE,EC,CF,AF,若四边形AECF为平行四边形,则BE=DF,请说明理由.