题目内容
1.解不等式(组).(1)5x+20≥0(把解集在数轴上表示出来)
(2)$\frac{x}{2}-1<\frac{x+1}{5}$
(3)1≤-2x+5≤3
(4)$\left\{\begin{array}{l}\frac{x}{3}-1<0\\ \frac{x}{2}+1>\frac{x}{3}\end{array}\right.$.
分析 (1)先移项,再合并同类项,系数化为1即可.
(2)先去分母,移项,再合并同类项,系数化为1即可.
(3)原式可转化为一个不等式组,先求出两个不等式的解集,再求其公共解.
(4)根据不等式的性质求出不等式的解集,根据找不等式组解集的规律找出即可.
解答 解:(1)5x+20≥0,
移项得,5x≥-20,
系数化为1得,x≥-4.
在数轴上表示为: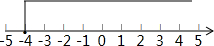
(2)$\frac{x}{2}-1<\frac{x+1}{5}$,
去分母得,5x-10<2x+2,
移项得,5x-2x<2+10,
合并同类项得,3x<12,
系数化为1得,x<4.
(3)1≤-2x+5≤3,
把不等式化为不等式组$\left\{\begin{array}{l}{1≤-2x+5①}\\{-2x+5≤3②}\end{array}\right.$,
由不等式①得x≤2,
由不等式②得x≥1,
所以不等组的解集为1≤x≤2;
(4)$\left\{\begin{array}{l}{\frac{x}{3}-1<0①}\\{\frac{x}{2}+1>\frac{x}{3}②}\end{array}\right.$,
由不等式①得x<3,
由不等式②得x>-6,
所以不等组的解集为-6<x<3.
点评 本题主要考查对不等式的性质,解一元一次不等式(组)等知识点的理解和掌握,能根据不等式的解集找出不等式组的解集是解此题的关键.

练习册系列答案
相关题目
11.下列二次根式中,最简二次根式是( )
| A. | $\sqrt{\frac{1}{3}}$ | B. | $\sqrt{0.3}$ | C. | $\sqrt{{a^2}+3}$ | D. | $\sqrt{a{b^2}}$ |
6.若x2+kx+81是一个完全平方式,则k等于( )
| A. | -18 | B. | 9 | C. | 18或-18 | D. | 18 |
13.下列式子中,是最简二次根式的是( )
| A. | $\sqrt{\frac{1}{4}}$ | B. | $\sqrt{30}$ | C. | $\sqrt{{x}^{3}}$ | D. | $\sqrt{27a}$ |
10.若平行四边形ABCD的周长为28cm,△ABC的周长为17cm,则AC的长为( )
| A. | 5.5cm | B. | 3cm | C. | 4cm | D. | 11cm |
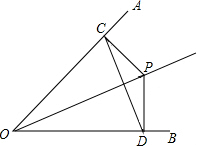 如图,已知P点是∠AOB平分线上一点,PC⊥OA,PD⊥OB,垂足为C、D.
如图,已知P点是∠AOB平分线上一点,PC⊥OA,PD⊥OB,垂足为C、D. 将直尺和三角板按如图的样子叠放在一起,则∠1+∠2的度数是90°.
将直尺和三角板按如图的样子叠放在一起,则∠1+∠2的度数是90°.