题目内容
数学课上,老师出示了如下框中的题目

小敏与同桌小聪讨论后,进行了如下解答:
(1)特殊情况•探索结论
当点E为AB的中点时,如图1,确定线段AE与DB的大小关系.请你直接写出结论:AE DB(填“>”,“<”或“=”).

(2)特例启发,解答题目
解:题目中,AE与DB的大小关系是:AE DB(填“>”,“<”或“=”)理由如下:如图2,过点E作EF∥BC,交AC于点F,(请你接着继续完成以下解答过程)
(3)拓展结论,设计新题
在等边三角形ABC中,点E在直线上AB上,点D在直线BC上,且ED=EC.若△ABC的边长为3,AE=5,求CD的长(请你直接写出结果).

小敏与同桌小聪讨论后,进行了如下解答:
(1)特殊情况•探索结论
当点E为AB的中点时,如图1,确定线段AE与DB的大小关系.请你直接写出结论:AE

(2)特例启发,解答题目
解:题目中,AE与DB的大小关系是:AE
(3)拓展结论,设计新题
在等边三角形ABC中,点E在直线上AB上,点D在直线BC上,且ED=EC.若△ABC的边长为3,AE=5,求CD的长(请你直接写出结果).
考点:全等三角形的判定与性质,等边三角形的性质
专题:
分析:(1)根据等边三角形的性质和三角形的内角和定理求出∠D=∠ECB=30°,求出∠D=∠DEB,求出DB=BE,BE=AE,即可得出答案;
(2)作EF∥BC,证△DBE≌△EFC,推出AE=EF=DB,即可得出答案;
(3)分为四种情况:画出图形,根据等边三角形的性质求出CD即可.
(2)作EF∥BC,证△DBE≌△EFC,推出AE=EF=DB,即可得出答案;
(3)分为四种情况:画出图形,根据等边三角形的性质求出CD即可.
解答:解:(1)答案为:=.
(2)答案为:=.
证明:在等边△ABC中,∠ABC=∠ACB=∠BAC=60°,AB=BC=AC,
∵EF∥BC,
∴∠AEF=∠ABC,∠AFE=∠ACB,
∴∠AEF=∠AFE=∠BAC=60°,
∴AE=AF=EF,
∴AB-AE=AC-AF,
即BE=CF,
∵∠ABC=∠EDB+∠BED,∠ACB=∠ECB+∠FCE,
∵ED=EC,
∴∠EDB=∠ECB,
∵∠EBC=∠EDB+∠BED,∠ACB=∠ECB+∠FCE,
∵ED=EC,
∴∠EDB=∠ECB,
∵∠EBC=∠EDB+∠BED,∠ACB=∠ECB+∠FCE,
∴∠BED=∠FCE,
在△DBE和△EFC中
,
∴△DBE≌△EFC(SAS),
∴DB=EF,
∴AE=BD,
故答案为:=.
(3)解:分为四种情况:
第一种情况:如图1:

∵AB=AC=3,AE=5,
∴B是AE的中点,
∵△ABC是等边三角形,
∴AB=AC=BC=3,△ACE是直角三角形(根据直角三角形斜边的中线等于斜边的一半),
∴∠ACE=90°,∠AEC=30°,
∴∠D=∠ECB=∠BEC=30°,∠DBE=∠ABC=60°,
∴∠DEB=180°-30°-60°=90°,
即△DEB是直角三角形.
∴BD=2BE=4(30°所对的直角边等于斜边的一半),
即CD=3+4=7.
第二种情况:如图2,

过A作AN⊥BC于N,过E作EM⊥CD于M,
∵等边三角形ABC,EC=ED,
∴BN=CN=
BC=
,BM=
BE=
×(3+5)=4,CM=MD=4-3=1,AN∥EM,
∴CD=2CM=2;
第三种情况:如图3,

∵∠ECD>∠EBC(∠EBC=120°),而∠ECD不能大于120°,否则△EDC不符合三角形内角和定理,
∴此时不存在EC=ED;
第四种情况:如图4,

∵∠EDC<∠ABC,∠ECB>∠ACB,
又∵∠ABC=∠ACB=60°,
∴∠ECD>∠EDC,
即此时ED≠EC,
∴此时情况不存在,
答:CD的长是7或2.
(2)答案为:=.
证明:在等边△ABC中,∠ABC=∠ACB=∠BAC=60°,AB=BC=AC,
∵EF∥BC,
∴∠AEF=∠ABC,∠AFE=∠ACB,
∴∠AEF=∠AFE=∠BAC=60°,
∴AE=AF=EF,
∴AB-AE=AC-AF,
即BE=CF,
∵∠ABC=∠EDB+∠BED,∠ACB=∠ECB+∠FCE,
∵ED=EC,
∴∠EDB=∠ECB,
∵∠EBC=∠EDB+∠BED,∠ACB=∠ECB+∠FCE,
∵ED=EC,
∴∠EDB=∠ECB,
∵∠EBC=∠EDB+∠BED,∠ACB=∠ECB+∠FCE,
∴∠BED=∠FCE,
在△DBE和△EFC中
|
∴△DBE≌△EFC(SAS),
∴DB=EF,
∴AE=BD,
故答案为:=.
(3)解:分为四种情况:
第一种情况:如图1:

∵AB=AC=3,AE=5,
∴B是AE的中点,
∵△ABC是等边三角形,
∴AB=AC=BC=3,△ACE是直角三角形(根据直角三角形斜边的中线等于斜边的一半),
∴∠ACE=90°,∠AEC=30°,
∴∠D=∠ECB=∠BEC=30°,∠DBE=∠ABC=60°,
∴∠DEB=180°-30°-60°=90°,
即△DEB是直角三角形.
∴BD=2BE=4(30°所对的直角边等于斜边的一半),
即CD=3+4=7.
第二种情况:如图2,

过A作AN⊥BC于N,过E作EM⊥CD于M,
∵等边三角形ABC,EC=ED,
∴BN=CN=
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴CD=2CM=2;
第三种情况:如图3,

∵∠ECD>∠EBC(∠EBC=120°),而∠ECD不能大于120°,否则△EDC不符合三角形内角和定理,
∴此时不存在EC=ED;
第四种情况:如图4,

∵∠EDC<∠ABC,∠ECB>∠ACB,
又∵∠ABC=∠ACB=60°,
∴∠ECD>∠EDC,
即此时ED≠EC,
∴此时情况不存在,
答:CD的长是7或2.
点评:本题考查了全等三角形的性质和判定,三角形的内角和定理,等边三角形的性质和判定的理解和运用,能综合运用性质进行推理是解此题的关键.

练习册系列答案
相关题目
以下列各组长度的线段为边,能构成三角形的是( )
| A、3,4,8 |
| B、5,6,10 |
| C、5,6,11 |
| D、5,9,15 |
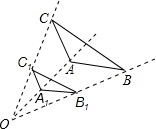 如图,△ABC和△A1B1C1是以点O为位似中心的位似三角形,若C1为OC的中点,AB=4,则A1B1的长为( )
如图,△ABC和△A1B1C1是以点O为位似中心的位似三角形,若C1为OC的中点,AB=4,则A1B1的长为( )