题目内容
⊙l为△ABC的内切圆,点D,E分别为边AB,AC上的点,且DE为⊙l的切线,若△ABC的周长为19,BC边的长为5,则△ADE的周长为 .
考点:三角形的内切圆与内心
专题:
分析:根据⊙l为△ABC的内切圆和切线长定理,即可求得DM=DN,EM=EH,BN=BG,CH=CG,又由△ABC的周长为19,BC边的长为5,即可求得AB+AC与BN+CH的值,继而求得△ADE的周长.
解答: 解:∵⊙l为△ABC的内切圆,
解:∵⊙l为△ABC的内切圆,
∴DM=DN,EM=EH,BN=BG,CH=CG,
∵△ABC的周长为19,BC边的长为5,
∴BG+CG=BN+CH=BC=5,AB+AC+BC=19,
∴AB+AC=19-BC=14,
∴△ADE的周长为:AD+DE+AE=AD+AE+AM+EM=AD+AE+DN+EH=AN+AH=AB+AC-BN-CH=(AB+AC)-(BN+CH)=14-5=9.
故答案为:9.
 解:∵⊙l为△ABC的内切圆,
解:∵⊙l为△ABC的内切圆,∴DM=DN,EM=EH,BN=BG,CH=CG,
∵△ABC的周长为19,BC边的长为5,
∴BG+CG=BN+CH=BC=5,AB+AC+BC=19,
∴AB+AC=19-BC=14,
∴△ADE的周长为:AD+DE+AE=AD+AE+AM+EM=AD+AE+DN+EH=AN+AH=AB+AC-BN-CH=(AB+AC)-(BN+CH)=14-5=9.
故答案为:9.
点评:本题考查了内切圆的性质与切线长定理的知识,此题难度适中,解题的关键是注意数形结合思想与整体思想的应用.

练习册系列答案
相关题目
 以下四个三角形,与如图的三角形相似的是( )
以下四个三角形,与如图的三角形相似的是( )A、 |
B、 |
C、 |
D、 |
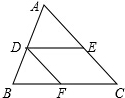 如图,在△ABC中,点D、E、F分别在AB、AC、BC上,DE∥BC,DF∥AC,下列比例式中,正确的是( )
如图,在△ABC中,点D、E、F分别在AB、AC、BC上,DE∥BC,DF∥AC,下列比例式中,正确的是( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 如图所示,最外侧大圆的面积是半径为2厘米的小圆面积的几倍?阴影部分的面积是半径为3厘米的圆的面积的多少?
如图所示,最外侧大圆的面积是半径为2厘米的小圆面积的几倍?阴影部分的面积是半径为3厘米的圆的面积的多少?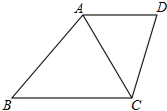 如图,在梯形ABCD中,AD∥BC,∠B=∠ACD,若AC=12,BC=16.
如图,在梯形ABCD中,AD∥BC,∠B=∠ACD,若AC=12,BC=16.