题目内容
矩形ABCD中，E、F分别为AB、CD中点，如果矩形ABCD与矩形EFCB相似，那么它们的相似比为（ ）
A、
| ||
B、
| ||
| C、2：1 | ||
| D、1：2 |
考点：相似多边形的性质
专题：计算题
分析：根据相似多边形的对应边之比，周长之比等于相似比，而面积之比等于相似比的平方．
解答：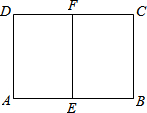
解：矩形ABCD对折后所得矩形与原矩形相似，
∵矩形ABCD∽矩形BCFE，
∵E、F分别为AB、CD的中点，
∴矩形ABCD的面积是矩形BCFE面积的2倍，
∴面积比是为：2：1，
设AD=b，AB=a，
∵E、F分别为AB、CD的中点，
∴
=
，
∴
=
，
∴a=
b，
∴
=
∵面积的比是相似比的平方，
∴相似比是
：1．
故选：A．
解：矩形ABCD对折后所得矩形与原矩形相似，∵矩形ABCD∽矩形BCFE，
∵E、F分别为AB、CD的中点，
∴矩形ABCD的面积是矩形BCFE面积的2倍，
∴面积比是为：2：1，
设AD=b，AB=a，
∵E、F分别为AB、CD的中点，
∴
| AD |
| AB |
| BE |
| BC |
∴
| b |
| a |
| ||
| b |
∴a=
| 2 |
∴
| AD |
| AB |
| b |
| a |
∵面积的比是相似比的平方，
∴相似比是
| 2 |
故选：A．
点评：本题考查相似多边形相似的性质及判定两个图形相似的依据：对应边的比相等，对应角相等，两个条件必须同时具备．
练习册系列答案
相关题目
直线AB上的点P到⊙O的圆心O的距离为5，⊙O的直径为10，则直线AB与⊙O的位置关系为（ ）
| A、相切 | B、相离 |
| C、相交 | D、相交或相切 |
用配方法将x2+4x+5变形的结果是（ ）
| A、（x-2）2+1 |
| B、（x+2）2+1 |
| C、（x-2）2+1 |
| D、（x+2）2-1 |
计算（-5）×（-5）的值是（ ）
| A、25 | B、-25 |
| C、10 | D、-10 |
下列结论正确的是（ ）
| A、等弧所对的圆心角相等 |
| B、同一条弦所对的两条弧一定是等弧 |
| C、相等的圆心角所对的弧相等 |
| D、长度相等的两条弧是等弧 |
下列二次根式中与
是同类二次根式的是（ ）
| 12 |
A、
| ||
B、
| ||
C、
| ||
D、
|
10名初中毕业生的中考体育考试成绩如下：26 29 26 25 26 26 27 28 29 30，这些成绩的中位数是
（ ）
（ ）
| A、25 | B、26 |
| C、26.5 | D、30 |