题目内容
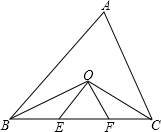如图，在△ABC中，已知AB=5，BC=6，∠ABC和∠ACB的角平分线BO与CO相交于点O，OE∥AB，OF∥AC，则△OEF的周长为考点：等腰三角形的判定与性质,平行线的性质
专题：几何图形问题
分析：根据角平分线的定义可得∠ABO=∠OBE，根据两直线平行，内错角相等可得∠ABO=∠BEO，然后求出∠OBE=∠BOE，再根据等角对等边可得BE=OE，同理可得CF=OF，然后求出△OEF的周长=BC，代值计算即可．
解答：解：∵BO平分∠ABC，
∴∠ABO=∠OBE，
∵OE∥AB，
∴∠ABO=∠BEO，
∴∠OBE=∠BOE，
∴BE=OE，
同理可得CF=OF，
∴△OEF的周长=OE+EF+OF=BE+EF+FC=BC，
∵BC=6，
∴△OEF的周长=6．
故答案为：6．
∴∠ABO=∠OBE，
∵OE∥AB，
∴∠ABO=∠BEO，
∴∠OBE=∠BOE，
∴BE=OE，
同理可得CF=OF，
∴△OEF的周长=OE+EF+OF=BE+EF+FC=BC，
∵BC=6，
∴△OEF的周长=6．
故答案为：6．
点评：本题考查了等腰三角形的判定与性质，角平分线的定义，平行线的性质，熟记定义与性质并求出△OEF的周长=BC是解题的关键．
练习册系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
如图，反比例函数y=
在△ABC中，∠BAC=2∠C，BD为∠ABC的平分线，BC=6，AB=3.5，则CD=
如图，在平面直角坐标系中，Rt△OAB的顶点A在x轴的正半轴上，顶点B的坐标为（3，
如图，