题目内容
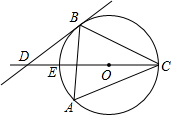 如图,在△ABC中,∠A=60°,⊙O是△ABC的外接圆,过点B作⊙O的切线,交CO的延长线于点D,CD交⊙O于点E.
如图,在△ABC中,∠A=60°,⊙O是△ABC的外接圆,过点B作⊙O的切线,交CO的延长线于点D,CD交⊙O于点E.(1)求证:BC=BD;
(2)若BC=3,求CD的长.
考点:切线的性质
专题:
分析:(1)连接BO、BE,可证明∠BDC=∠BCD=30°,从而得出结论;
(2)根据BD=BC,可得出BD=3,再由直角三角形的性质得出CD的长即可.
(2)根据BD=BC,可得出BD=3,再由直角三角形的性质得出CD的长即可.
解答: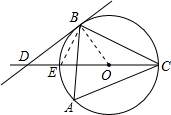 解:连接BO、BE,
解:连接BO、BE,
∵∠A=60°,
∴∠BOC=30°,
∵OB=OC,
∴∠OBC=30°
∵CE是直径,
∴∠CBE=90°,
∴∠CEB=60°,
∴∠OBE=60°,
∵BD为⊙O切线,
∴∠OBD=90°,
∴∠DBE=∠EDB=30°,
∴∠BDC=∠BCD=30°,
∴BC=BD;
(2)∵BC=BD,BC=3,
∴BD=3,
∵∠BCD=30°,
∴tan30°=
,
∴BE=
,
∴CE=2
,OB=
,
∴OD=2
,
∴CD=OD+OC=3
.
 解:连接BO、BE,
解:连接BO、BE,∵∠A=60°,
∴∠BOC=30°,
∵OB=OC,
∴∠OBC=30°
∵CE是直径,
∴∠CBE=90°,
∴∠CEB=60°,
∴∠OBE=60°,
∵BD为⊙O切线,
∴∠OBD=90°,
∴∠DBE=∠EDB=30°,
∴∠BDC=∠BCD=30°,
∴BC=BD;
(2)∵BC=BD,BC=3,
∴BD=3,
∵∠BCD=30°,
∴tan30°=
| BE |
| BC |
∴BE=
| 3 |
∴CE=2
| 3 |
| 3 |
∴OD=2
| 3 |
∴CD=OD+OC=3
| 3 |
点评:本题考查了切线的性质,解直角三角形以及勾股定理的综合运用,是重点内容,要熟练掌握.

练习册系列答案
相关题目
下列有关
叙述错误的是( )
| 3 |
A、
| ||||
B、
| ||||
C、1<
| ||||
D、
|
 如图,抛物线y=ax2-5ax+4a与x轴相交于点A、B,且过点C(5,4).
如图,抛物线y=ax2-5ax+4a与x轴相交于点A、B,且过点C(5,4).
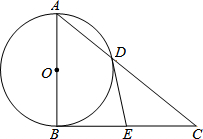 如图,Rt△ABC中,∠ABC=90°,以AB为直径的⊙O交AC于点D,E为BC边的中点,连接DE.
如图,Rt△ABC中,∠ABC=90°,以AB为直径的⊙O交AC于点D,E为BC边的中点,连接DE. 如图,已知△ABC,以AC为直径的⊙O交AB于点D,点E为弧
如图,已知△ABC,以AC为直径的⊙O交AB于点D,点E为弧
