题目内容
 如图,抛物线y=ax2-5ax+4a与x轴相交于点A、B,且过点C(5,4).
如图,抛物线y=ax2-5ax+4a与x轴相交于点A、B,且过点C(5,4).(1)求a的值和该抛物线顶点P的坐标;
(2)求三角形ABC的面积;
(3)将抛物线先向左平移2个单位,再向上平移3个单位,写出平移后抛物线的解析式.
考点:抛物线与x轴的交点,二次函数图象与几何变换
专题:
分析:(1)把点C的坐标代入函数解析式,列出关于系数a的方程,通过解方程来求a的值;
(2)由(1)中的解析式求得点A、B的坐标,然后求得线段AB的长度,结合三角形面积公式来求三角形ABC的面积;
(3)抛物线y=ax2+bx+c(a≠0)通过配方,将一般式化为y=a(x-h)2+k的形式,可确定其顶点坐标为(h,k);然后根据平移的规律直接写出平移后的抛物线解析式.
(2)由(1)中的解析式求得点A、B的坐标,然后求得线段AB的长度,结合三角形面积公式来求三角形ABC的面积;
(3)抛物线y=ax2+bx+c(a≠0)通过配方,将一般式化为y=a(x-h)2+k的形式,可确定其顶点坐标为(h,k);然后根据平移的规律直接写出平移后的抛物线解析式.
解答:解:(1)把点C(5,4)代入抛物线y=ax2-5ax+4a,
得25a-25a+4a=4,
解得a=1.
∴该二次函数的解析式为y=x2-5x+4.
∵y=x2-5x+4=(x-
)2-
,
∴顶点坐标为P(
,-
).
综上所述,a的值和该抛物线顶点P的坐标分别是1、(
,-
);
(2)∵由(1)知,二次函数的解析式为y=x2-5x+4=(x-1)(x-4).
则A(1,0),B(4,0).
∴AB=3.
又C(5,4),
∴三角形ABC的面积是:
×3×4=6;
(3)由抛物线y=(x-
)2-
先向左平移2个单位,再向上平移3个单位,
得到的二次函数解析式为y=(x-
+2)2-
+3=(x-
)2+
=x2-x+1,
即y=x2-x+1.
得25a-25a+4a=4,
解得a=1.
∴该二次函数的解析式为y=x2-5x+4.
∵y=x2-5x+4=(x-
| 5 |
| 2 |
| 9 |
| 4 |
∴顶点坐标为P(
| 5 |
| 2 |
| 9 |
| 4 |
综上所述,a的值和该抛物线顶点P的坐标分别是1、(
| 5 |
| 2 |
| 9 |
| 4 |
(2)∵由(1)知,二次函数的解析式为y=x2-5x+4=(x-1)(x-4).
则A(1,0),B(4,0).
∴AB=3.
又C(5,4),
∴三角形ABC的面积是:
| 1 |
| 2 |
(3)由抛物线y=(x-
| 5 |
| 2 |
| 9 |
| 4 |
得到的二次函数解析式为y=(x-
| 5 |
| 2 |
| 9 |
| 4 |
| 1 |
| 2 |
| 3 |
| 4 |
即y=x2-x+1.
点评:本题考查抛物线与x轴的交点及平移的有关知识.解题时,需要熟悉抛物线解析式的三种形式.

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
 如图,AB是⊙O的直径,四边形ABCD内接于⊙O,若BC=CD=6cm,∠ABD=30°,则⊙O的面积为( )
如图,AB是⊙O的直径,四边形ABCD内接于⊙O,若BC=CD=6cm,∠ABD=30°,则⊙O的面积为( )| A、25πcm2 |
| B、49πcm2 |
| C、32πcm2 |
| D、36πcm2 |
 如图所示,点D为△ABC的边AB的中点,且AD=CD.求证:∠ACB=90°.
如图所示,点D为△ABC的边AB的中点,且AD=CD.求证:∠ACB=90°. 已知△ABC,
已知△ABC, 如图,矩形ABCD中,BC=8,对角线BD=10,求tan∠ACB.
如图,矩形ABCD中,BC=8,对角线BD=10,求tan∠ACB.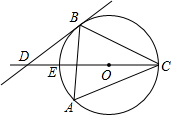 如图,在△ABC中,∠A=60°,⊙O是△ABC的外接圆,过点B作⊙O的切线,交CO的延长线于点D,CD交⊙O于点E.
如图,在△ABC中,∠A=60°,⊙O是△ABC的外接圆,过点B作⊙O的切线,交CO的延长线于点D,CD交⊙O于点E.