题目内容
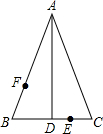如图，AD是等腰△ABC的顶角平分线，E、F分别是DC、AB上的点，求作点E、F关于直线AD的对称点．
考点：作图-轴对称变换
专题：
分析：利用等腰三角形的性质可得出AD⊥BC，BD=DC，进而得出点E、F关于直线AD的对称点．
解答：
解：如图所示：
∵AD是等腰△ABC的顶角平分线，
∴AD⊥BC，BD=DC，
∴点E关于直线AD的对称点为E′，点F关于直线AD的对称点为F′．
解：如图所示：∵AD是等腰△ABC的顶角平分线，
∴AD⊥BC，BD=DC，
∴点E关于直线AD的对称点为E′，点F关于直线AD的对称点为F′．
点评：此题主要考查了作轴对称变换，正确利用等腰三角形的性质得出是解题关键．
练习册系列答案
周周清检测系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
如图，在以BD为直径的⊙O上， |
| AB |
|
| BC |
| A、70° | B、30° |
| C、35° | D、40° |
把方程3x（x-1）=5（x+2）化为一般形式正确的是（ ）
| A、3x2-3x-10=0 |
| B、3x2-8x-10=0 |
| C、3x2-8x+10=0 |
| D、x2-3x-10=0 |
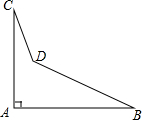一个零件的形状如图，按规定∠A应等于90°，∠B与∠C应分别是32°和21°，检验工人量得∠BDC=148°，就判断这个零件不合格，试用三角形的有关知识说明理由．