题目内容
7．求证：2222+3111能被7整除．分析 将原式转化为4111+3111，根据a2n+1+b2n+1能被a+b整除得到4111+3111能被（4+3）整除，从而得证．
解答 证明：2222+3111=（22）111+3111=4111+3111，
∵a2n+1+b2n+1能被a+b整除，
∴4111+3111能被（4+3）整除，
∴2222+3111能被7整除．
点评 本题考查了数的整除性，解题的关键是了解a2n+1+b2n+1能被a+b整除，难度中等．
练习册系列答案
相关题目
12．如果式子m-7与4m-9互为相反数，则m的值为（ ）
| A． | $\frac{16}{3}$ | B． | -$\frac{16}{3}$ | C． | $\frac{16}{5}$ | D． | -$\frac{16}{5}$ |
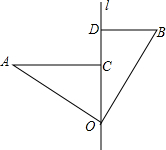如图，∠AOB=90°，OA=OB，直线l经过点O，分别过A、B两点作AC⊥l交l于点C，BD⊥l交l于点D．若AC=10，BD=6，则CD=4．