题目内容
8.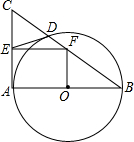 如图所示,以Rt△ABC的直角边AB为直径⊙O交BC边于D点,过D点作⊙O的切线交AC边于E点,又过E点作EF∥AB交BC于F点.若AB=20,CD=9,则OF=$\frac{15}{2}$.
如图所示,以Rt△ABC的直角边AB为直径⊙O交BC边于D点,过D点作⊙O的切线交AC边于E点,又过E点作EF∥AB交BC于F点.若AB=20,CD=9,则OF=$\frac{15}{2}$.
分析 首先连接AD,由射影定理得AB2=BD•BC,易得BD,得BC,由勾股定理得AC,由切线长定理得AE=DE,易得E为AC的中点,EF为△ABC的中位线,证得四边形AEFO为矩形,得OF=AE=$\frac{1}{2}AC$.
解答  解:连接AD,
解:连接AD,
∵AB为直径,
∴∠ADB=90°,
∵∠BAC=90°,
∴AB2=BD•BC,
设BD=x,则BC=9+x,
∴202=x•(x+9),解得:x1=-25(不合题意,舍去),x2=16,
∴BD=16,
∴BC=25,
∴AC=$\sqrt{B{C}^{2}-A{B}^{2}}$=$\sqrt{2{5}^{2}-2{0}^{2}}$=15,
∵DE为⊙O的切线,
∵∠BAC=90°,
∴AC为⊙O的切线,
∴DE=AE,
∴∠EAD=∠EDA,
∵∠EAD+∠C=90°,∠EDA+∠CDE=90°,
∴∠C=∠CDE,
∴CE=DE,
∴E为AC的中点,
∵EF∥AB,
∴F为BC的中点,
∴EF=$\frac{1}{2}AB$=AO,
∴四边形AEFO为矩形,
∴OF=AE=$\frac{1}{2}$AC=$\frac{15}{2}$,
故答案为:$\frac{15}{2}$.
点评 本题主要考查了切线的性质及判定,三角形中位线的性质,证得四边形AEFO为矩形是解答此题的关键.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
20.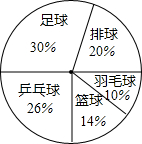 某学校七年级三班有50名学生,现对学生最喜欢的球类运动进行了调查,根据调查的结果制作了扇形统计图,如图所示.根据扇形统计图中提供的信息,给出以下结论,正确的是( )
某学校七年级三班有50名学生,现对学生最喜欢的球类运动进行了调查,根据调查的结果制作了扇形统计图,如图所示.根据扇形统计图中提供的信息,给出以下结论,正确的是( )
 某学校七年级三班有50名学生,现对学生最喜欢的球类运动进行了调查,根据调查的结果制作了扇形统计图,如图所示.根据扇形统计图中提供的信息,给出以下结论,正确的是( )
某学校七年级三班有50名学生,现对学生最喜欢的球类运动进行了调查,根据调查的结果制作了扇形统计图,如图所示.根据扇形统计图中提供的信息,给出以下结论,正确的是( )| A. | 最喜欢足球的人数是15人 | B. | 最喜欢羽毛球的人数是4人 | ||
| C. | 最喜欢排球的人数是20人 | D. | 最喜欢乒乓球的人数是26人 |
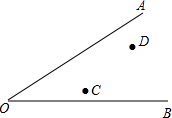 如图,C、D是∠AOB内部两点,在∠AOB内部求作一点P,使PC=PD,并且使点P到∠AOB两边的距离相等(要求:不写作法,保留作图痕迹)
如图,C、D是∠AOB内部两点,在∠AOB内部求作一点P,使PC=PD,并且使点P到∠AOB两边的距离相等(要求:不写作法,保留作图痕迹) 如图,函数y=ax+4和y=bx的图象相交于点A,则不等式ax+4<0的解集为x>7,不等式bx≥ax+4的解集为x≥2.
如图,函数y=ax+4和y=bx的图象相交于点A,则不等式ax+4<0的解集为x>7,不等式bx≥ax+4的解集为x≥2.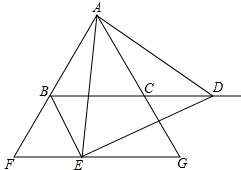 如图:△ABC是等边三角形,点D是射线BC上的一个动点(点D不与点B、C重合),△ADE是以AD为边的等边三角形,过点E作BC的平行线,分别交射线AB、AC于点F、G,连接BE.
如图:△ABC是等边三角形,点D是射线BC上的一个动点(点D不与点B、C重合),△ADE是以AD为边的等边三角形,过点E作BC的平行线,分别交射线AB、AC于点F、G,连接BE.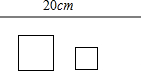 刘老师在数学课上给出了一个情景:如图,将一根长为20cm的铁丝剪成两段,以每一段为周长各围成一个正方形.
刘老师在数学课上给出了一个情景:如图,将一根长为20cm的铁丝剪成两段,以每一段为周长各围成一个正方形.