题目内容
16. 如图,函数y=ax+4和y=bx的图象相交于点A,则不等式ax+4<0的解集为x>7,不等式bx≥ax+4的解集为x≥2.
如图,函数y=ax+4和y=bx的图象相交于点A,则不等式ax+4<0的解集为x>7,不等式bx≥ax+4的解集为x≥2.
分析 从图象上找出y=ax+4的图象在x轴下方所对应的自变量的范围即可得到不等式ax+4<0的解集;当x≥2时,直线y=bx都不在直线y=ax+4的下方,于是可得到不等式bx≥ax+4的解集.
解答 解:当x>7时,y=ax+4<0,
所以不等式ax+4<0的解集为x>7;
当x≥2时,bx≥ax+4,
所以不等式bx≥ax+4的解集为x≥2.
故答案为x>7,x≥2.
点评 本题考查了一次函数与一元一次不等式:一次函数与一元一次不等式的关系从函数的角度看,就是寻求使一次函数y=kx+b的值大于(或小于)0的自变量x的取值范围;从函数图象的角度看,就是确定直线y=kx+b在x轴上(或下)方部分所有的点的横坐标所构成的集合.

练习册系列答案
相关题目
6.下列根式中能与$\sqrt{3}$合并的是( )
| A. | $\sqrt{6}$ | B. | $\sqrt{9}$ | C. | $\sqrt{12}$ | D. | $\sqrt{18}$ |
4.下列各式从左到右的变形为分解因式的是( )
| A. | m2-m-6=(m+2)(m-3) | B. | (m+2)(m-3)=m2-m-6 | ||
| C. | x2+8x-9=(x+3)(m-3)+8x | D. | 18x3y2=3x3y2•6 |
1.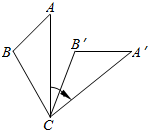 如图,将△ABC绕着点C顺时针旋转50°后得到△A′B′C′.若∠A=40°,∠B′=110°,则∠BCA′的度数是( )
如图,将△ABC绕着点C顺时针旋转50°后得到△A′B′C′.若∠A=40°,∠B′=110°,则∠BCA′的度数是( )
 如图,将△ABC绕着点C顺时针旋转50°后得到△A′B′C′.若∠A=40°,∠B′=110°,则∠BCA′的度数是( )
如图,将△ABC绕着点C顺时针旋转50°后得到△A′B′C′.若∠A=40°,∠B′=110°,则∠BCA′的度数是( )| A. | 90° | B. | 80° | C. | 50° | D. | 30° |
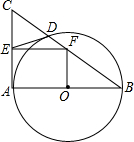 如图所示,以Rt△ABC的直角边AB为直径⊙O交BC边于D点,过D点作⊙O的切线交AC边于E点,又过E点作EF∥AB交BC于F点.若AB=20,CD=9,则OF=$\frac{15}{2}$.
如图所示,以Rt△ABC的直角边AB为直径⊙O交BC边于D点,过D点作⊙O的切线交AC边于E点,又过E点作EF∥AB交BC于F点.若AB=20,CD=9,则OF=$\frac{15}{2}$.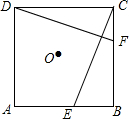 如图,E、F分别是正方形ABCD的边AB、BC上的点,且BE=CF,连接CE、DF,将△DCF绕着正方形的中心O按顺时针方向旋转到△CBE的位置,则旋转角为( )
如图,E、F分别是正方形ABCD的边AB、BC上的点,且BE=CF,连接CE、DF,将△DCF绕着正方形的中心O按顺时针方向旋转到△CBE的位置,则旋转角为( )