题目内容
17.解不等式组:$\left\{\begin{array}{l}{\frac{2x+1}{3}≥-3}\\{1-2x>7}\end{array}\right.$.分析 分别解出两不等式的解集再求其公共解.
解答 解:$\left\{\begin{array}{l}\frac{2x+1}{3}≥-3…(1)\\ 1-2x>7\;\;…(2)\end{array}\right.$
由(1)解得:x≥-5,
由(2)解得:x<-3.
故原不等式组的解集是-5≤x<-3.
点评 本题主要考查了一元一次不等式组解集的求法,其简便求法就是用口诀求解.求不等式组解集的口诀:同大取大,同小取小,大小小大中间找,大大小小找不到(无解).

练习册系列答案
相关题目
6.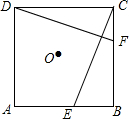 如图,E、F分别是正方形ABCD的边AB、BC上的点,且BE=CF,连接CE、DF,将△DCF绕着正方形的中心O按顺时针方向旋转到△CBE的位置,则旋转角为( )
如图,E、F分别是正方形ABCD的边AB、BC上的点,且BE=CF,连接CE、DF,将△DCF绕着正方形的中心O按顺时针方向旋转到△CBE的位置,则旋转角为( )
 如图,E、F分别是正方形ABCD的边AB、BC上的点,且BE=CF,连接CE、DF,将△DCF绕着正方形的中心O按顺时针方向旋转到△CBE的位置,则旋转角为( )
如图,E、F分别是正方形ABCD的边AB、BC上的点,且BE=CF,连接CE、DF,将△DCF绕着正方形的中心O按顺时针方向旋转到△CBE的位置,则旋转角为( )| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
3. 如图,将矩形ABCO放在直角坐标系中,其中顶点B的坐标为(10,8),E是BC边上一点,将△ABE沿AE折叠,点B刚好与OC边上点D重合,过点E的反比例函数y=$\frac{k}{x}$的图象与边AB交于点F,则线段AF的长为( )
如图,将矩形ABCO放在直角坐标系中,其中顶点B的坐标为(10,8),E是BC边上一点,将△ABE沿AE折叠,点B刚好与OC边上点D重合,过点E的反比例函数y=$\frac{k}{x}$的图象与边AB交于点F,则线段AF的长为( )
 如图,将矩形ABCO放在直角坐标系中,其中顶点B的坐标为(10,8),E是BC边上一点,将△ABE沿AE折叠,点B刚好与OC边上点D重合,过点E的反比例函数y=$\frac{k}{x}$的图象与边AB交于点F,则线段AF的长为( )
如图,将矩形ABCO放在直角坐标系中,其中顶点B的坐标为(10,8),E是BC边上一点,将△ABE沿AE折叠,点B刚好与OC边上点D重合,过点E的反比例函数y=$\frac{k}{x}$的图象与边AB交于点F,则线段AF的长为( )| A. | $\frac{15}{4}$ | B. | 2 | C. | $\frac{15}{8}$ | D. | $\frac{3}{2}$ |
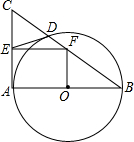 如图所示,以Rt△ABC的直角边AB为直径⊙O交BC边于D点,过D点作⊙O的切线交AC边于E点,又过E点作EF∥AB交BC于F点.若AB=20,CD=9,则OF=$\frac{15}{2}$.
如图所示,以Rt△ABC的直角边AB为直径⊙O交BC边于D点,过D点作⊙O的切线交AC边于E点,又过E点作EF∥AB交BC于F点.若AB=20,CD=9,则OF=$\frac{15}{2}$. 如图,已知m∥n,将一块等边三角形ABC纸板放置在平行线之间,则∠1-∠2等于60度.
如图,已知m∥n,将一块等边三角形ABC纸板放置在平行线之间,则∠1-∠2等于60度.