Question

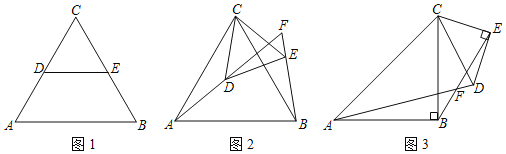
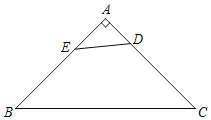
【题目】如图，在等腰直角△ABC中，AB＝4，点D是边AC上一点，且AD＝1，点E是AB边上一点，连接DE，以线段DE为直角边作等腰直角△DEF（D、E、F三点依次呈逆时针方向），当点F恰好落在BC边上时，则AE的长是_____．

Answer 1

【答案】或2

【解析】

分两种情况：①当∠DEF＝90°时，证明△CDF∽△BFE，得出，求出BF＝，得出CF＝BC﹣BF＝，得出BE＝，即可得出答案；

②当∠EDF＝90°时，同①得△CDF∽△BFE，得出，求出BF＝CD＝3，得出CF＝BC﹣BF＝，得出BE＝CF＝2，即可得出答案．

解：分两种情况：

①当∠DEF＝90°时，如图1所示：

∵△ABC和△DEF是等腰直角三角形，

∴AC＝AB＝4，∠B＝∠C＝∠EFD＝∠EDF＝45°，BC＝AB＝4，DF＝EF，

∵AD＝1，

∴CD＝AC﹣AD＝3，

∵∠EFC＝∠EFD+∠CFD＝∠B+∠BEF，

∴∠CFD＝∠BEF，

∴△CDF∽△BFE，

∴，

∴BF＝，

∴CF＝BC﹣BF＝4﹣＝，

∴BE＝＝，

∴AE＝AB﹣BE＝；

②当∠EDF＝90°时，如图2所示：

同①得：△CDF∽△BFE，

∴，

∴BF＝CD＝3，

∴CF＝BC﹣BF＝4﹣3＝，

∴BE＝CF＝2，

∴AE＝AB﹣BE＝2；

综上所述，AE的长是或2；

故答案为：或2．