Question

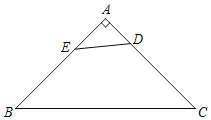
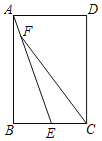
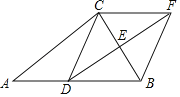
【题目】在Rt△ABC中，∠ACB＝90°，点D、E分别是AB、BC的中点，过点C作CF∥AB，与DE的延长线并交于点F，连接BF．

（1）试判断四边形CDBF的形状，并说明理由；

（2）若CD＝5，sin∠CAB＝，过点C作CH⊥BF，垂足为H点，试求CH的长．

Answer 1

【答案】（1）四边形CDBF是菱形，见解析；（2）CH＝．

【解析】

（1）证出DE是△ABC的中位线，得出DE∥AC，AC＝2DE，证出四边形CDBF是平行四边形，由直角三角形的性质得出CD＝AB＝BD，即可得出四边形CDBF是菱形；

（2）由直角三角形的性质得出AB＝2CD＝10，求出BC＝6，由勾股定理得出AC＝＝8，得出DE＝AC＝4，由菱形的性质得出DF＝2DE＝8，BF＝CD＝5，由菱形CDBF的面积即可得出结果．

解：（1）四边形CDBF是菱形，理由如下：

∵点D、E分别是AB、BC的中点，

∴DE是△ABC的中位线，

∴DE∥AC，AC＝2DE，

∴DF∥AC，

∵CF∥AB，

∴四边形CDBF是平行四边形，

∵∠ACB＝90°，点D是AB的中点，

∴CD＝AB＝BD，

∴四边形CDBF是菱形；

（2）如图所示：

∵∠ACB＝90°，CD＝5，

∴AB＝2CD＝10，

∵sin∠CAB＝＝，

∴BC＝6，

∴AC＝＝8，

∴DE＝AC＝4，

∵四边形CDBF是菱形，

∴DF＝2DE＝8，BF＝CD＝5，

∵菱形CDBF的面积＝BF×CH＝×BC×DF＝×6×8＝24，

∴CH＝．