Question

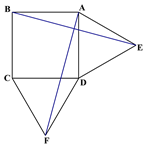
【题目】如图,平行四边形ABCD中,∠BDC=30°，DC=4,AE⊥BD于E，CF⊥BD于F，且E、F恰好是BD的三等分点，AE、CF的延长线分别交DC、AB于N、M点,那么四边形MENF的面积是( )

A.B.C.2D.2

Answer 1

【答案】B

【解析】

由已知条件可得EN与EF的长，进而可得Rt△NEF的面积，即可求解四边形MENF的面积．

解：∵E，F为BD的三等分点，

∴DE=EF=BF，

∵AE⊥BD，CF⊥BD，

∴EN∥FC，

∴EN是△DFC的中位线，

∴EN=FC.

∵在Rt△DCF中，∠BDC=30°，DC=4，

∴FC=2，

∴EN=1，

∴在Rt△DEN中，∠EDN=30°，

∴DN=2EN=2，DE==，

∴EF=DE=，

∴S△ENF= ×1×=，

四边形MENF的面积=×2=.

故选B.