题目内容
8.已知点A在半径为3的⊙O内,OA等于1,点B是⊙O上一点,连接AB,当∠OBA取最大值时,AB长度为( )| A. | $\sqrt{10}$ | B. | 2$\sqrt{2}$ | C. | 3 | D. | 2 |
分析 当AB⊥OA时,AB取最小值,∠OBA取得最大值,然后在直角三角形OBA中利用勾股定理求PA的值即可.
解答 解:在△OBA中,当∠OBA取最大值时,OA取最大值,
∴BA取最小值,
又∵OA、OB是定值,
∴BA⊥OA时,BA取最小值;
在直角三角形OBA中,OA=1,OB=3,
∴AB=$\sqrt{9-1}$=2$\sqrt{2}$.
故选B.
点评 本题考查了解直角三角形.解答此题的关键是找出“当BA⊥OA时,BA取最小值”即“BA⊥OA时,∠OBA取最大值”这一隐含条件.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

 如图表示两辆汽车行驶路程与时间的关系(汽车B在汽车A后出发)的图象,试回答下列问题:
如图表示两辆汽车行驶路程与时间的关系(汽车B在汽车A后出发)的图象,试回答下列问题: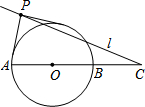 如图,已知⊙O的半径为2,C为直径AB延长线上一点,BC=2.过C任作一直线l.若l上总存在点P,使过P所作的⊙O的两切线互相垂直,则∠ACP的最大值等于45°.
如图,已知⊙O的半径为2,C为直径AB延长线上一点,BC=2.过C任作一直线l.若l上总存在点P,使过P所作的⊙O的两切线互相垂直,则∠ACP的最大值等于45°. 如图,AB是⊙O的一条弦,点C是⊙O上一动点,且$\widehat{AB}$=60°,点E、F分别是AC、BC的中点,直线EF与⊙O交于G,H两点.若⊙O的半径为6,则GE+FH的最大值为9.
如图,AB是⊙O的一条弦,点C是⊙O上一动点,且$\widehat{AB}$=60°,点E、F分别是AC、BC的中点,直线EF与⊙O交于G,H两点.若⊙O的半径为6,则GE+FH的最大值为9. 如图,梯形ABCD中,AB∥CD,∠ABC=90°,AB=8,CD=6,BC=4,AB边上有一动点P(不与A、B重合),连结DP,作PQ⊥DP,使得PQ交线段BC于点E,设AP=x.
如图,梯形ABCD中,AB∥CD,∠ABC=90°,AB=8,CD=6,BC=4,AB边上有一动点P(不与A、B重合),连结DP,作PQ⊥DP,使得PQ交线段BC于点E,设AP=x. 用4个棱长为1的正方体搭成一个几何模型,其从正面、左面看到的图形如图所示,则该几何体从上面看到的图形不可能为( )
用4个棱长为1的正方体搭成一个几何模型,其从正面、左面看到的图形如图所示,则该几何体从上面看到的图形不可能为( )


