题目内容
13.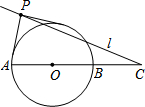 如图,已知⊙O的半径为2,C为直径AB延长线上一点,BC=2.过C任作一直线l.若l上总存在点P,使过P所作的⊙O的两切线互相垂直,则∠ACP的最大值等于45°.
如图,已知⊙O的半径为2,C为直径AB延长线上一点,BC=2.过C任作一直线l.若l上总存在点P,使过P所作的⊙O的两切线互相垂直,则∠ACP的最大值等于45°.
分析 根据切线的性质和已知条件先证得四边形PMON是正方形,从而求得OP=2$\sqrt{2}$,以O为圆心,以2$\sqrt{2}$长为半径作大圆⊙O,然后过C点作大⊙O的切线,切点即为P点,此时∠ACP有最大值,作出图形,根据切线的性质得出OP⊥PC,根据勾股定理求得PC的长,从而证得△OPC是等腰直角三角形,即可证得∠ACP的最大值为45°.
解答 解:∵PM、PN是过P所作的⊙O的两切线且互相垂直,
∴∠MON=90°,
∴四边形PMON是正方形,
根据勾股定理求得OP=2$\sqrt{2}$,
∴P点在以O为圆心,以2$\sqrt{2}$长为半径作大圆⊙O上,
以O为圆心,以2$\sqrt{2}$长为半径作大圆⊙O,然后过C点作大⊙O的切线,切点即为P点,此时∠ACP有最大值,如图所示,
∵PC是大圆⊙O的切线,
∴OP⊥PC, ∵OC=4,OP=2$\sqrt{2}$,
∵OC=4,OP=2$\sqrt{2}$,
∴PC=$\sqrt{O{C}^{2}-O{P}^{2}}$=2$\sqrt{2}$,
∴OP=PC,
∴∠ACP=45°,
∴∠ACP的最大值等于45°,.
故答案为45°.
点评 本题考查了切线的性质,正方形的判定和性质,勾股定理的应用,解题的关键是求得P点的位置.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
17.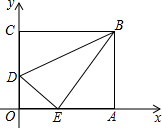 如图所示,把矩形OABC放入平面直角坐标系中,点B坐标为(10,8),点D是OC上一动点,将矩形OABC沿直线BD折叠,点C恰好落在OA上的点E处,则点D的坐标是( )
如图所示,把矩形OABC放入平面直角坐标系中,点B坐标为(10,8),点D是OC上一动点,将矩形OABC沿直线BD折叠,点C恰好落在OA上的点E处,则点D的坐标是( )
 如图所示,把矩形OABC放入平面直角坐标系中,点B坐标为(10,8),点D是OC上一动点,将矩形OABC沿直线BD折叠,点C恰好落在OA上的点E处,则点D的坐标是( )
如图所示,把矩形OABC放入平面直角坐标系中,点B坐标为(10,8),点D是OC上一动点,将矩形OABC沿直线BD折叠,点C恰好落在OA上的点E处,则点D的坐标是( )| A. | (0,4) | B. | (0,5) | C. | (0,3) | D. | (3,0) |
18. 如图,该表面展开图按虚线折叠成正方体后,相对面上的两个数互为相反数,则(x+y)的值为( )
如图,该表面展开图按虚线折叠成正方体后,相对面上的两个数互为相反数,则(x+y)的值为( )
 如图,该表面展开图按虚线折叠成正方体后,相对面上的两个数互为相反数,则(x+y)的值为( )
如图,该表面展开图按虚线折叠成正方体后,相对面上的两个数互为相反数,则(x+y)的值为( )| A. | -2 | B. | -3 | C. | 2 | D. | 1 |
8.已知点A在半径为3的⊙O内,OA等于1,点B是⊙O上一点,连接AB,当∠OBA取最大值时,AB长度为( )
| A. | $\sqrt{10}$ | B. | 2$\sqrt{2}$ | C. | 3 | D. | 2 |
18. 一个大正方形和四个全等的小正方形按图①、②两种方式摆放,则图②的大正方形中未被小正方形覆盖部分的面积为( )
一个大正方形和四个全等的小正方形按图①、②两种方式摆放,则图②的大正方形中未被小正方形覆盖部分的面积为( )
 一个大正方形和四个全等的小正方形按图①、②两种方式摆放,则图②的大正方形中未被小正方形覆盖部分的面积为( )
一个大正方形和四个全等的小正方形按图①、②两种方式摆放,则图②的大正方形中未被小正方形覆盖部分的面积为( )| A. | a-b | B. | a+b | C. | ab | D. | a2-ab |
 三个全等的直角梯形①、②、③在平面直角坐标系中的位置如图所示,抛物线y=ax2+bx+c经过梯形的顶点A、B、C、D,已知梯形的两条底边长分别为4,6,则梯形的两腰长分别为2、2$\sqrt{2}$,该抛物线解析式为y=$-\frac{1}{4}{x}^{2}+\frac{1}{2}x+6$.
三个全等的直角梯形①、②、③在平面直角坐标系中的位置如图所示,抛物线y=ax2+bx+c经过梯形的顶点A、B、C、D,已知梯形的两条底边长分别为4,6,则梯形的两腰长分别为2、2$\sqrt{2}$,该抛物线解析式为y=$-\frac{1}{4}{x}^{2}+\frac{1}{2}x+6$.
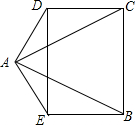 如图,AB=AC,AD=AE,∠DAB=∠EAC,DE=CB.
如图,AB=AC,AD=AE,∠DAB=∠EAC,DE=CB.