Question

如图，在直角△ABC中，∠C=90°，∠B=30°，AB的垂直平分线交AB于点D，交BC于点E，若AC=

3

，CE=1，则△DBE的周长为（　　）

• A、1+

  3

• B、2+

  3

• C、2

  3

  +1
• D、3+

  3

Answer 1

考点：线段垂直平分线的性质,含30度角的直角三角形

专题：

分析：如图，连接AE．则由“垂直平分线上任意一点，到线段两端点的距离相等”推知BE=AE；在直角△ABC中、直角△ACE中，利用30度所对的直角边是斜边的一半得到：AC=

1

2

AB、CE=

1

2

AE，故△DBE的周长=AC+AE+BE．

解答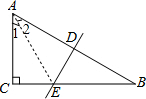：解：∵在直角△ACE中，AC=

3

，CE=1，
∴由勾股定理知 AE=

AC2+CE2

=2，
如图，连接AE．
∵DE是线段AB的垂直平分线，
∴AE=BE．
∴∠2=∠B．
又在直角△ABC中，∠C=90°，∠B=30°，
∴∠CAD=60°，∠2=∠B=30°．
∴∠1=∠2=30°，AB=2AC，
∴CE=DE=

1

2

AE=1．
∴△DBE的周长=

1

2

AB+BE+DE=AC+AE+DE=

3

+2+1=3+

3

．
故选：D．

点评：此题考查了线段垂直平分线的性质、等角对等边的性质、角平分线的性质．由已知条件结合各知识点得到结论对选项逐一验证时解答本题的关键