题目内容
如图，在平面直角坐标系xOy中，O是坐标原点，已知A（3，2），B（-2，3），则∠OAB等于考点：勾股定理的逆定理,两点间的距离公式
专题：
分析：连接OB，根据点的坐标分别求出OB，OA，AB的长，再根据勾股定理的逆定理可得△OAB为等腰直角三角形，根据等腰直角三角形的性质即可求解．
解答：
解：连接OB．
则OA=
=
，OB=
=
，AB=
=
．
∵（
）2+（
）2=（
）2，
∴△OAB为等腰直角三角形，
∴∠OAB=45°．
故答案为：45．
解：连接OB．则OA=
| 32+22 |
| 13 |
| 32+22 |
| 13 |
| (3+2)2+(2-3)2 |
| 26 |
∵（
| 13 |
| 13 |
| 26 |
∴△OAB为等腰直角三角形，
∴∠OAB=45°．
故答案为：45．
点评：此题考查了平面直角坐标系两点间的距离公式，勾股定理的逆定理，等腰直角三角形的判定和性质．
练习册系列答案
名校课堂系列答案
相关题目
如图，直线AB、CD相交于点O，过点O作两条射线OM、ON，且∠AOM=∠CON=90°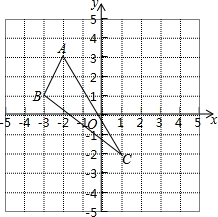
在平面直角坐标系中，△ABC的三个顶点位置如图所示．
如图，在直角△ABC中，∠C=90°，∠B=30°，AB的垂直平分线交AB于点D，交BC于点E，若AC=| 3 |
A、1+
| ||
B、2+
| ||
C、2
| ||
D、3+
|
某计算程序编辑如图所示，当输入x=