题目内容
11.下列各组线段中,能够组成直角三角形的一组是( )| A. | 1,2,3 | B. | 2,3,4 | C. | 4,5,6 | D. | 1,$\sqrt{2}$,$\sqrt{3}$ |
分析 根据勾股定理的逆定理:如果三角形有两边的平方和等于第三边的平方,那么这个三角形是直角三角形判定则可.
解答 解:A、12+22≠32,不能组成直角三角形,故错误;
B、22+32≠42,不能组成直角三角形,故错误;
C、42+52≠62,不能组成直角三角形,故错误;
D、12+($\sqrt{2}$)2=($\sqrt{3}$)2,能够组成直角三角形,故正确.
故选D.
点评 本题考查了勾股定理的逆定理,在应用勾股定理的逆定理时,应先认真分析所给边的大小关系,确定最大边后,再验证两条较小边的平方和与最大边的平方之间的关系,进而作出判断.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2. 如图所示,AH∥DG∥BC,DF∥AC,图中和∠ACB相等的角(不包括自身)有( )
如图所示,AH∥DG∥BC,DF∥AC,图中和∠ACB相等的角(不包括自身)有( )
 如图所示,AH∥DG∥BC,DF∥AC,图中和∠ACB相等的角(不包括自身)有( )
如图所示,AH∥DG∥BC,DF∥AC,图中和∠ACB相等的角(不包括自身)有( )| A. | 3个 | B. | 4个 | C. | 5个 | D. | 6个 |
6.已知数据:2,4,2,5,7.则这组数据的众数和中位数分别是( )
| A. | 2,2 | B. | 2,4 | C. | 2,5 | D. | 4,4 |
3.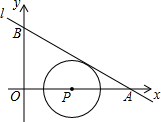 我们将在直角坐标系中圆心坐标和半径均为整数的圆称为“整圆”.如图,直线l:y=kx+4$\sqrt{3}$与x轴、y轴分别交于A、B,∠OAB=30°,点P在x轴上,⊙P与l相切,当P在线段OA上运动时,使得⊙P成为整圆的点P个数是( )
我们将在直角坐标系中圆心坐标和半径均为整数的圆称为“整圆”.如图,直线l:y=kx+4$\sqrt{3}$与x轴、y轴分别交于A、B,∠OAB=30°,点P在x轴上,⊙P与l相切,当P在线段OA上运动时,使得⊙P成为整圆的点P个数是( )
 我们将在直角坐标系中圆心坐标和半径均为整数的圆称为“整圆”.如图,直线l:y=kx+4$\sqrt{3}$与x轴、y轴分别交于A、B,∠OAB=30°,点P在x轴上,⊙P与l相切,当P在线段OA上运动时,使得⊙P成为整圆的点P个数是( )
我们将在直角坐标系中圆心坐标和半径均为整数的圆称为“整圆”.如图,直线l:y=kx+4$\sqrt{3}$与x轴、y轴分别交于A、B,∠OAB=30°,点P在x轴上,⊙P与l相切,当P在线段OA上运动时,使得⊙P成为整圆的点P个数是( )| A. | 6 | B. | 8 | C. | 10 | D. | 12 |
20.使$\sqrt{x-1}$有意义的x的取值范围是( )
| A. | x≠1 | B. | x≥1 | C. | x>1 | D. | x≥0 |
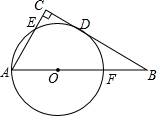 如图,在△ABC中,∠C=90°,以AB上一点O为圆心,OA长为半径的圆恰好与BC相切于点D,分别交AC、AB于点E、F.
如图,在△ABC中,∠C=90°,以AB上一点O为圆心,OA长为半径的圆恰好与BC相切于点D,分别交AC、AB于点E、F. 如图,在△ABC中,CD平分∠ACB交AB于点D,DE⊥AC交于点E,DF⊥BC于点F,且BC=4,DE=2,则△BCD的面积是4.
如图,在△ABC中,CD平分∠ACB交AB于点D,DE⊥AC交于点E,DF⊥BC于点F,且BC=4,DE=2,则△BCD的面积是4.