题目内容
4.设N=88888888写成十进制数时,它的各位数字之和是A,而A的各位数字之和是B,B的各位数字之和是C.则C是( )| A. | 11 | B. | 7 | C. | 9 | D. | 4 |
分析 根据一个十进制数被9除余几,它的各位数字之和被9除也余几;又因为一个数被9除余1,它的任意正整数次幂被9除也余1,得出N,A,B,C被9除的余数相同,再分析N除9的余数,最后根据N的位数得出A的范围,再根据A的范围确定出B的范围,进而得出C的范围,最后利用余数即可得出结论.
解答 解:由于一个十进制数被9除余几,它的各位数字之和被9除也余几;
又因为一个数被9除余1,它的任意正整数次幂被9除也余1,这样就有N,A,B,C被9除的余数相同,
N=88888888=88888•11118888,
而88888=644444,64除以9余1,
∴644444除以9也余1,
即88888除以9也余1,
∵11118888=(1107×9+4)8888=9k1+48888,而48888=48886×16=642962×16,
因此,642962除以9余1,而16除以9余7,即:48888除以9余7,
∴11118888除以9余7,从而N除以9余7,
∴N,A,B,C除以9均余7,
∵N的位数小于4×8888=35552,
因此,N的各位数字之和A<9×35552=319968,
而小于319968的多位数的各位数字之和最大是2+5×9=47,
即B≤47,而小于等于47的数的各位数字之和最大是3+9=12,
从而C≤12,又C除以9余7,
故C=7,
故选B.
点评 此题是带余除法,解本题的根据是十进制数被9除余几,它的各位数字之和被9除也余几和一个数被9除余1,它的任意正整数次幂被9除也余1;是一道难度比较大的竞赛题.

练习册系列答案
 53天天练系列答案
53天天练系列答案
相关题目
16.1米长的小棒,第1次截去一半,第2次截去剩下的一半,如此下去,第6次后剩下的小棒长为( )
| A. | $\frac{1}{12}$ | B. | $\frac{1}{32}$ | C. | $\frac{1}{64}$ | D. | $\frac{1}{128}$ |
13.已知⊙O的半径为2cm,弦AB长为2cm,则这条弦的中点到弦所对优弧中点的距离为( )
| A. | 2cm | B. | $\sqrt{3}$cm | C. | (2-$\sqrt{3}$)cm | D. | (2+$\sqrt{3}$)cm |
14.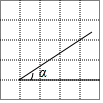 在5×5网格中,∠α的位置如图所示,则tanα的值是( )
在5×5网格中,∠α的位置如图所示,则tanα的值是( )
 在5×5网格中,∠α的位置如图所示,则tanα的值是( )
在5×5网格中,∠α的位置如图所示,则tanα的值是( )| A. | 2 | B. | $\frac{1}{2}$ | C. | $\frac{3}{2}$ | D. | $\frac{2}{3}$ |
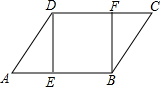 如图,在平行四边形ABCD中,E、F分别是AB、DC上的点,且AE=CF,求证:
如图,在平行四边形ABCD中,E、F分别是AB、DC上的点,且AE=CF,求证: