题目内容
16.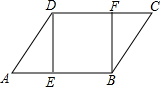 如图,在平行四边形ABCD中,E、F分别是AB、DC上的点,且AE=CF,求证:
如图,在平行四边形ABCD中,E、F分别是AB、DC上的点,且AE=CF,求证:(1)证明△ADE≌△CBF;
(2)当∠DEB=90°时,试说明四边形DEBF为矩形.
分析 (1)利用平行四边形的性质,根据SAS即可证明.
(2)首先证明四边形DEBF是矩形,由∠DEB=90°,即可推出四边形DEBF是矩形.
解答 证明:(1)∵四边形ABCD是平行四边形,
∴AD=CB,∠A=∠C,
在△ADE和△CBF中,
$\left\{\begin{array}{l}{AD=CB}\\{∠A=∠C}\\{AE=CF}\end{array}\right.$,
∴△ADE≌△CBF(SAS).
(2)∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,
∵AE=CF,
∴BE=DF,
∴四边形DEBF是平行四边形,
∵∠DEB=90°,
∴四边形DEBF是矩形.
点评 本题考查矩形的判定和性质、平行四边形的性质、全等三角形的判定和性质等知识,解题的关键灵活运用所学知识解决问题,属于中考常考题型.

练习册系列答案
相关题目
4.2017的相反数是( )
| A. | 2017 | B. | -2017 | C. | $\frac{1}{2017}$ | D. | -$\frac{1}{2017}$ |
11.若(x-1)0=1,则( )
| A. | x≥1 | B. | x≤1 | C. | x≠1 | D. | x≠0 |
 如图,在△ABC中,∠ACB=90°,CD⊥AB于D
如图,在△ABC中,∠ACB=90°,CD⊥AB于D 小明、小华从学校出发到青少年宫参加书法比赛,小明步行一段时间后,小华骑自行车沿相同路线行进,两人均匀速前行.他们的路程差s (米)与小明出发时间t (分)之间的函数关系如图所示.下列说法:
小明、小华从学校出发到青少年宫参加书法比赛,小明步行一段时间后,小华骑自行车沿相同路线行进,两人均匀速前行.他们的路程差s (米)与小明出发时间t (分)之间的函数关系如图所示.下列说法: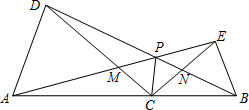 如图,C为线段AB上的任意一点(不与点A,B重合),分别以AC,BC为一腰在AB的同侧作等腰三角形ACD和等腰三角形BCE,CA=CD,CB=CE,∠ACD与∠BCE都是锐角且∠ACD=∠BCE,连接AE交CD于点M,连接BD交CE于点N,AE与BD相交于点P,连接PC.求证:△ACE≌△DCB.
如图,C为线段AB上的任意一点(不与点A,B重合),分别以AC,BC为一腰在AB的同侧作等腰三角形ACD和等腰三角形BCE,CA=CD,CB=CE,∠ACD与∠BCE都是锐角且∠ACD=∠BCE,连接AE交CD于点M,连接BD交CE于点N,AE与BD相交于点P,连接PC.求证:△ACE≌△DCB.