题目内容
2. 如图,AB是⊙O的直径,C,E是⊙O上的两点,CD⊥AB于D,交BE于F,$\widehat{BC}$=$\widehat{EC}$.求证:BF=CF.
如图,AB是⊙O的直径,C,E是⊙O上的两点,CD⊥AB于D,交BE于F,$\widehat{BC}$=$\widehat{EC}$.求证:BF=CF.
分析 延长CD交⊙O于点G,连接BC,根据垂径定理证明即可.
解答 证明:延长CD交⊙O于点G,连接BC,
∵AB是⊙O的直径,CD⊥AB于D
∴$\widehat{BC}$=$\widehat{BG}$,
∵$\widehat{BC}$=$\widehat{EC}$
∴$\widehat{BG}$=$\widehat{EC}$
∴∠BCF=∠CBF,
∴BF=CF.
点评 本题考查了等腰三角形的性质,垂径定理,圆周角定理等知识点的应用,解此题的关键是作辅助线后根据定理求出∠CBE=∠BCE,通过做此题培养了学生分析问题和解决问题的能力,题型较好.

练习册系列答案
相关题目
12. 如图,正方形ABCD的边长为2,E是CD的中点,将△ADE绕点A按顺时针方向旋转后得到△ABF,则EF的长等于( )
如图,正方形ABCD的边长为2,E是CD的中点,将△ADE绕点A按顺时针方向旋转后得到△ABF,则EF的长等于( )
 如图,正方形ABCD的边长为2,E是CD的中点,将△ADE绕点A按顺时针方向旋转后得到△ABF,则EF的长等于( )
如图,正方形ABCD的边长为2,E是CD的中点,将△ADE绕点A按顺时针方向旋转后得到△ABF,则EF的长等于( )| A. | 3 | B. | $\sqrt{10}$ | C. | 2$\sqrt{5}$ | D. | 3$\sqrt{2}$ |
10. 如图,数轴上表示-2.75的点是( )
如图,数轴上表示-2.75的点是( )
 如图,数轴上表示-2.75的点是( )
如图,数轴上表示-2.75的点是( )| A. | 点A | B. | 点B | C. | 点C | D. | 点D |
7.下列各选项中的两项是同类项的为( )
| A. | -ab2与-$\frac{1}{2}$a2b | B. | 32与-53 | C. | x2与-y2 | D. | 3xy3与2x2y2 |
14.2016年10月10日,山东移动4G用户突破3000万,3000万用科学记数法可表示为( )
| A. | 0.3×108 | B. | 3×107 | C. | 3×106 | D. | 3×103 |
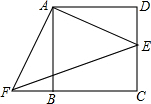
 如图,在矩形ABCD中,点E、F分别在边AD、DC上,BE⊥EF,AB=6,AE=9,DE=2,求DF的长.
如图,在矩形ABCD中,点E、F分别在边AD、DC上,BE⊥EF,AB=6,AE=9,DE=2,求DF的长.