题目内容
12.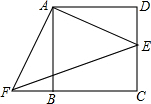 如图,正方形ABCD的边长为2,E是CD的中点,将△ADE绕点A按顺时针方向旋转后得到△ABF,则EF的长等于( )
如图,正方形ABCD的边长为2,E是CD的中点,将△ADE绕点A按顺时针方向旋转后得到△ABF,则EF的长等于( )| A. | 3 | B. | $\sqrt{10}$ | C. | 2$\sqrt{5}$ | D. | 3$\sqrt{2}$ |
分析 先利用勾股定理计算出AE,再根据旋转的性质得∠EAF=∠BAD=90°,AE=AF,则可判断△AEF为等腰直角三角形,然后根据等腰直角三角形的性质计算EF的长.
解答 解:∵四边形ABCD为正方形,
∴∠BAD=∠D=90°,
在Rt△ADE中,AE=$\sqrt{D{E}^{2}+A{D}^{2}}$=$\sqrt{{1}^{2}+{2}^{2}}$=$\sqrt{5}$,
∵△ADE绕点A按顺时针方向旋转后得到△ABF,
∴∠EAF=∠BAD=90°,AE=AF,
∴△AEF为等腰直角三角形,
∴EF=$\sqrt{2}$AE=$\sqrt{10}$.
故选B.
点评 本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
3.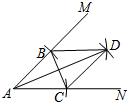 如图,以A点为圆心,以相同的长为半径作弧,分别与射线AM,AN交于B,C两点,连接BC,再分别以B,C为圆心,以相同长(大于$\frac{1}{2}$BC)为半径作弧,两弧相交于点D,连接AD,BD,CD.则下列结论错误的是( )
如图,以A点为圆心,以相同的长为半径作弧,分别与射线AM,AN交于B,C两点,连接BC,再分别以B,C为圆心,以相同长(大于$\frac{1}{2}$BC)为半径作弧,两弧相交于点D,连接AD,BD,CD.则下列结论错误的是( )
 如图,以A点为圆心,以相同的长为半径作弧,分别与射线AM,AN交于B,C两点,连接BC,再分别以B,C为圆心,以相同长(大于$\frac{1}{2}$BC)为半径作弧,两弧相交于点D,连接AD,BD,CD.则下列结论错误的是( )
如图,以A点为圆心,以相同的长为半径作弧,分别与射线AM,AN交于B,C两点,连接BC,再分别以B,C为圆心,以相同长(大于$\frac{1}{2}$BC)为半径作弧,两弧相交于点D,连接AD,BD,CD.则下列结论错误的是( )| A. | AD平分∠MAN | B. | AD垂直平分BC | ||
| C. | ∠MBD=∠NCD | D. | 四边形ACDB一定是菱形 |
4.单项式-$\frac{{2}^{3}{a}^{2}b}{5}$的次数是( )
| A. | -23 | B. | -$\frac{8}{5}$ | C. | 6 | D. | 3 |
1. 如图,数轴上A、B两点分别对应实数a、b,则下列结论错误的是( )
如图,数轴上A、B两点分别对应实数a、b,则下列结论错误的是( )
 如图,数轴上A、B两点分别对应实数a、b,则下列结论错误的是( )
如图,数轴上A、B两点分别对应实数a、b,则下列结论错误的是( )| A. | a+b<0 | B. | a2>b2 | C. | ab<0 | D. | |a|<|b| |
 如图,AC=6cm,BD=9cm,D是AC的中点,则AB=12cm.
如图,AC=6cm,BD=9cm,D是AC的中点,则AB=12cm.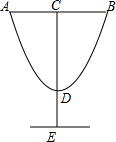 设计师以y=2x2-4x+8的图形为灵感设计杯子如图所示,若AB=4,DE=3,则杯子的高CE=11.
设计师以y=2x2-4x+8的图形为灵感设计杯子如图所示,若AB=4,DE=3,则杯子的高CE=11. 一条排水管的截面如图所示.已知排水管的半径OB=10,水面宽AB=16.求截面圆心O到水面的距离.
一条排水管的截面如图所示.已知排水管的半径OB=10,水面宽AB=16.求截面圆心O到水面的距离.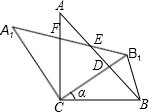 如图,△ABC中,∠ACB=90°,AC=BC=1,将△ABC绕点C逆时针旋转得到△A1B1C,旋转角为ɑ(0°<ɑ<90°),连接BB1.设CB1交AB于点D,A1B1分别交AB、AC于点E,F.
如图,△ABC中,∠ACB=90°,AC=BC=1,将△ABC绕点C逆时针旋转得到△A1B1C,旋转角为ɑ(0°<ɑ<90°),连接BB1.设CB1交AB于点D,A1B1分别交AB、AC于点E,F. 如图,AB是⊙O的直径,C,E是⊙O上的两点,CD⊥AB于D,交BE于F,$\widehat{BC}$=$\widehat{EC}$.求证:BF=CF.
如图,AB是⊙O的直径,C,E是⊙O上的两点,CD⊥AB于D,交BE于F,$\widehat{BC}$=$\widehat{EC}$.求证:BF=CF.