题目内容
8. 已知:如图,在△ABC中,点D、F在边AB上,点E在边AC上,且DE∥BC,AD2=AB•AF,求证:$\frac{EF}{CD}$=$\frac{DE}{BC}$.
已知:如图,在△ABC中,点D、F在边AB上,点E在边AC上,且DE∥BC,AD2=AB•AF,求证:$\frac{EF}{CD}$=$\frac{DE}{BC}$.
分析 由DE∥BC,可证得△ADE∽△ABC,然后由相似三角形的对应边成比例,证得AD:AB=DE:BC=AE:AC,又由AD2=AB•AF,可证得△AFE∽△ADC,继而证得结论.
解答 证明:∵DE∥BC,
∴△ADE∽△ABC,
∴AD:AB=DE:BC=AE:AC,
∵AD2=AB•AF,
∴AD:AB=AF:AD,
∴AF:AD=AE:AC,
∵∠A=∠A,
∴△AFE∽△ADC,
∴EF:CD=AE:AC,
∴$\frac{EF}{CD}$=$\frac{DE}{BC}$.
点评 此题考查了相似三角形的判定与性质.注意证得△ADE∽△ABC与△AFE∽△ADC是关键.

练习册系列答案
 名题金卷系列答案
名题金卷系列答案
相关题目
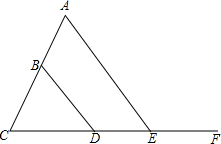 如图,在△BCD中,若AE∥BD,∠A=55°,∠BDE=125°,求∠C的度数.
如图,在△BCD中,若AE∥BD,∠A=55°,∠BDE=125°,求∠C的度数. 已知:如图,在Rt△ABC中,∠C=90°,∠B=30°,AD平分∠BAC.求证:点D在AB的垂直平分线上.
已知:如图,在Rt△ABC中,∠C=90°,∠B=30°,AD平分∠BAC.求证:点D在AB的垂直平分线上.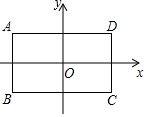 如图,分别以长方形ABCD的两条对称轴为x轴和y轴建立平面直角坐标系,若A点的坐标为(-4,3).
如图,分别以长方形ABCD的两条对称轴为x轴和y轴建立平面直角坐标系,若A点的坐标为(-4,3).