题目内容
19．
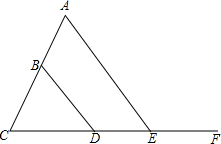如图，在△BCD中，若AE∥BD，∠A=55°，∠BDE=125°，求∠C的度数．
分析 根据邻补角定义可得∠CDB=180°-125°=55°，根据平行线的性质可得∠CBD=∠A=55°，然后再利用三角形内角和定理计算出∠C的度数．
解答 解：∵∠BDE=125°，
∴∠CDB=180°-125°=55°，
∵AE∥BD，∠A=55°，
∴∠CBD=55°，
∴∠C=180°-55°-55°=70°．
点评 此题主要考查了平行线的性质和三角形内角和定理，关键是掌握两直线平行，同位角相等．
练习册系列答案
黄冈天天练口算题卡系列答案
相关题目
如图，P在∠AOB内，点M、N分别是点P关于AO、BO的对称点，MN分 别交OA、OB于E、F．
如图，二次函数y=-x2+3x+m的图象与x轴的一个交点为B（4，0），另一个交点为A，且与y轴相交于C点．
如图，已知等边△ABC的边长为6，折叠△ABC，使得点A恰好与边BC上的点D重合，折痕为EF（点E、F分别在边AB、AC上）
已知：如图，在△ABC中，点D、F在边AB上，点E在边AC上，且DE∥BC，AD2=AB•AF，求证：$\frac{EF}{CD}$=$\frac{DE}{BC}$．
如图，自行车的车身为三角结构，这样做根据的数学道理是三角形具有稳定性．