题目内容
 如图,点C是半圆O的半径OB上的动点,作PC⊥AB于点C,点D是半圆上位于PC左侧的点,连结BD交线段PC于E,且PD=PE.
如图,点C是半圆O的半径OB上的动点,作PC⊥AB于点C,点D是半圆上位于PC左侧的点,连结BD交线段PC于E,且PD=PE.(1)若⊙O的半径为4,PC=8,OC=1,求∠B的正切值与正弦值;
(2)连结AD,求AD的长.
考点:切线的判定与性质,相似三角形的判定与性质
专题:
分析:(1)连接OD、OP,先证明∠PDO=90°,然后根据勾股定理求得OP的长,进而根据勾股定理求得PE的长,即可求得CE的长,根据勾股定理求得EB的长,从而求得∠B的正切值与正弦值;
(2)根据圆周角的性质求得∠ADB=90°利用∠B的正弦值和AB的长即可求得AD的长.
(2)根据圆周角的性质求得∠ADB=90°利用∠B的正弦值和AB的长即可求得AD的长.
解答: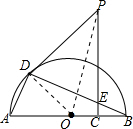 解:(1)连接OD、OP,
解:(1)连接OD、OP,
∵OB=OD,
∴∠OBD=∠ODB.
∵PD=PE,
∴∠PDE=∠PED.
∴∠PDO=∠PDE+∠ODE
=∠PED+∠OBD
=∠BEC+∠OBD
=90°,
∴PD⊥OD.
∴PD是⊙O的切线.
在Rt△POC中,
OP2=OC2+PC2=1+64=65.
在Rt△PDO中,
PD2=OP2-OD2=65-16=49.
∴PD=7,
∵PD=PE.
∴PE=7,
∴EC=PC-PE=8-7=1,
∴BE=
=
=
,
∴tanB=
=
,sinB=
=
=
;
(2)∵AB是直径,
∴∠ADB=90°,
∴sinB=
,
∴AD=AB•sinB=8×
=
.
 解:(1)连接OD、OP,
解:(1)连接OD、OP,∵OB=OD,
∴∠OBD=∠ODB.
∵PD=PE,
∴∠PDE=∠PED.
∴∠PDO=∠PDE+∠ODE
=∠PED+∠OBD
=∠BEC+∠OBD
=90°,
∴PD⊥OD.
∴PD是⊙O的切线.
在Rt△POC中,
OP2=OC2+PC2=1+64=65.
在Rt△PDO中,
PD2=OP2-OD2=65-16=49.
∴PD=7,
∵PD=PE.
∴PE=7,
∴EC=PC-PE=8-7=1,
∴BE=
| CE2+CB2 |
| 1+32 |
| 10 |
∴tanB=
| CE |
| CB |
| 1 |
| 3 |
| CE |
| EB |
| 1 | ||
|
| ||
| 10 |
(2)∵AB是直径,
∴∠ADB=90°,
∴sinB=
| AD |
| AB |
∴AD=AB•sinB=8×
| ||
| 10 |
4
| ||
| 5 |
点评:本题考查了切线的判定和性质,勾股定理的应用及综合解直角三角形的能力.

练习册系列答案
 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
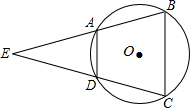 如图,已知⊙O外一点E,过E作两条射线分别交⊙O于A、B、C、D四点,若AE=DE,求证:
如图,已知⊙O外一点E,过E作两条射线分别交⊙O于A、B、C、D四点,若AE=DE,求证:
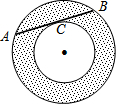 如图,两个同心圆⊙O,大圆弦AB切小圆于一点C,AB=8,则图中圆环(即阴影部分)的面积
如图,两个同心圆⊙O,大圆弦AB切小圆于一点C,AB=8,则图中圆环(即阴影部分)的面积 已知,如图,AC=AD,BC=BD,O为AB上一点,
已知,如图,AC=AD,BC=BD,O为AB上一点,