题目内容
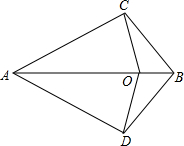 已知,如图,AC=AD,BC=BD,O为AB上一点,
已知,如图,AC=AD,BC=BD,O为AB上一点,求证:OC=OD.
考点:全等三角形的判定与性质
专题:证明题
分析:利用“边边边”证明△ABC和△ABD全等,根据全等三角形对应角相等可得∠BAC=∠BAD,再利用“边角边”证明△AOC和△AOD全等,根据全等三角形对应边相等可得OC=OD.
解答:证明:在△ABC和△ABD中,
,
∴△ABC≌△ABD(SSS),
∴∠BAC=∠BAD,
在△AOC和△AOD中,
,
∴△AOC≌△AOD(SAS),
∴OC=OD.
|
∴△ABC≌△ABD(SSS),
∴∠BAC=∠BAD,
在△AOC和△AOD中,
|
∴△AOC≌△AOD(SAS),
∴OC=OD.
点评:本题考查了全等三角形的判定与性质,熟练掌握三角形全等的判定方法是解题的关键,难点在于二次证明三角形全等.

练习册系列答案
相关题目
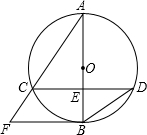 如图,已知⊙O的直径AB与弦CD互相垂直,垂足为E.⊙O的切线BF与弦AC的延长线相交于点F,且AC=8,tan∠BDC=
如图,已知⊙O的直径AB与弦CD互相垂直,垂足为E.⊙O的切线BF与弦AC的延长线相交于点F,且AC=8,tan∠BDC= 如图,点C是半圆O的半径OB上的动点,作PC⊥AB于点C,点D是半圆上位于PC左侧的点,连结BD交线段PC于E,且PD=PE.
如图,点C是半圆O的半径OB上的动点,作PC⊥AB于点C,点D是半圆上位于PC左侧的点,连结BD交线段PC于E,且PD=PE.