题目内容
如图，已知二次函数y1=ax2+bx+c（a≠0）与一次函数y2=kx+m（k≠0）的图象相交于点A（-2，4），B（8，2），则关于x的不等式ax2+（b-k）x+c-m＜0的解集是（ ）| A、-2≤x≤8 |
| B、2＜x＜4 |
| C、-2＜x＜8 |
| D、-2＜x＜4 |
考点：二次函数与不等式（组）
专题：
分析：把不等式整理成ax2+bx+c＜kx+m，再根据函数图象写出二次函数图象在一次函数图象下方部分的x的取值范围即可．
解答：解：ax2+（b-k）x+c-m＜0可化为ax2+bx+c＜kx+m，
∵交点A（-2，4），B（8，2），
∴不等式的解集是-2＜x＜8．
故选C．
∵交点A（-2，4），B（8，2），
∴不等式的解集是-2＜x＜8．
故选C．
点评：本题考查了二次函数与不等式，把不等式整理成两个函数解析式的形式是解题的关键．
练习册系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案
小学暑假作业东南大学出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案
相关题目
有理数a、b在数轴上的对应的位置如图所示：则a+b
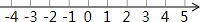已知在纸面上有一数轴（如图），折叠纸面．例如：若数轴上数2表示的点与数-2表示的点重合，则数轴上数-4表示的点与数4表示的点重合，根据你对例题的理解，解答下列问题：