题目内容
18.在反比例函数y=$\frac{1-2m}{x}$的图象上有两点A(x1,y1)(x2,y2),当x2>x1>0时,有y2>y1,则m的取值范围是( )| A. | m<0 | B. | m>0 | C. | m<$\frac{1}{2}$ | D. | m>$\frac{1}{2}$ |
分析 根据反比例函数图象上点的坐标特征得到x1•y1=1-2m,x2•y2=1-2m,而x2>x1>0时,有y2>y1,则1-2m<0,然后解不等式即可.
解答 解:∵点(x1,y1)(x2,y2)都在反比例函数y=$\frac{1-2m}{x}$的图象上,
∴x1•y1=1-2m,x2•y2=1-2m,
而x2>x1>0时,有y2>y1,
∴1-2m<0,
∴m>$\frac{1}{2}$.
故选D.
点评 本题考查了反比例函数图象上点的坐标特征:反比例函数y=$\frac{k}{x}$(k为常数,k≠0)的图象是双曲线,图象上的点(x,y)的横纵坐标的积是定值k,即xy=k.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
9.如图图形既是轴对称图形又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
6.某蒜苔生产基地收获蒜苔200吨.计划采用批发、零售、冷库储藏后销售三种方式出售,计划平均每吨的售价及成本如表:
经过一段时间,蒜苔按计划全部售出获得的总利润为y(元),蒜苔零售x(吨),且零售量是批发量的$\frac{1}{3}$.
(l)求y与x之间的函数关系式;
(2)由于受条件限制,经冷库储藏售出的蒜苔最多80吨,求该生产基地全部售完蒜苔获得的最大利润.
| 销售方式 | 批发 | 零售 | 储藏后销售 |
| 售价(元/吨) | 3000 | 4500 | 5500 |
| 成本(元/吨) | 700 | 1000 | 1200 |
(l)求y与x之间的函数关系式;
(2)由于受条件限制,经冷库储藏售出的蒜苔最多80吨,求该生产基地全部售完蒜苔获得的最大利润.
3.厦门市2014年中考体育考试中,某校九年级(3)班50人参加考试,具体的成绩与人数如表,则该班的中考体育的平均成绩是23.6分.
| 成绩 | 人数 |
| 25 | 24 |
| 24 | 10 |
| 22 | 10 |
| 20 | 6 |

 如图,在10×10的网格中,每个小方格都是边长为1的小正方形,每个小正方形的顶点称为格点.若抛物线经过图中的三个格点,则以这三个格点为顶点的三角形称为抛物线的“内接格点三角形”.以O为坐标原点建立如图所示的平面直角坐标系,若抛物线与网格对角线OB的两个交点之间的距离为3$\sqrt{2}$,且这两个交点与抛物线的顶点是抛物线的内接格点三角形的三个顶点,则满足上述条件且对称轴平行于y轴的抛物线条数是14.
如图,在10×10的网格中,每个小方格都是边长为1的小正方形,每个小正方形的顶点称为格点.若抛物线经过图中的三个格点,则以这三个格点为顶点的三角形称为抛物线的“内接格点三角形”.以O为坐标原点建立如图所示的平面直角坐标系,若抛物线与网格对角线OB的两个交点之间的距离为3$\sqrt{2}$,且这两个交点与抛物线的顶点是抛物线的内接格点三角形的三个顶点,则满足上述条件且对称轴平行于y轴的抛物线条数是14. 如图,已知⊙O与BC相切,点C不是切点,AO⊥OC,∠OAC=∠ABO,且AC=BO,判断直线AB与⊙O的位置关系,并说明理由.
如图,已知⊙O与BC相切,点C不是切点,AO⊥OC,∠OAC=∠ABO,且AC=BO,判断直线AB与⊙O的位置关系,并说明理由.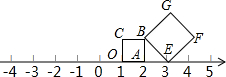 已知正方形OABC,BEFG,按照如图所示位置摆放在数轴上,点O、A、E表示的数分别为1、2、3,若以O为圆心,OF为半径作圆弧,则与数轴的交点表示的数为$\sqrt{10}+1$、-$\sqrt{10}+1$.
已知正方形OABC,BEFG,按照如图所示位置摆放在数轴上,点O、A、E表示的数分别为1、2、3,若以O为圆心,OF为半径作圆弧,则与数轴的交点表示的数为$\sqrt{10}+1$、-$\sqrt{10}+1$.