题目内容
10. 如图,已知⊙O与BC相切,点C不是切点,AO⊥OC,∠OAC=∠ABO,且AC=BO,判断直线AB与⊙O的位置关系,并说明理由.
如图,已知⊙O与BC相切,点C不是切点,AO⊥OC,∠OAC=∠ABO,且AC=BO,判断直线AB与⊙O的位置关系,并说明理由.
分析 延长BA至D,使得BD=OA,连结OD,通过SAS证明△OAC≌△DBO,根据全等三角形的性质可得OC=OD,∠ODB=∠OCA=90°,再根据直线与圆的位置关系即可求解.
解答 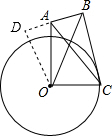 解:延长BA至D,使得BD=OA,连结OD,
解:延长BA至D,使得BD=OA,连结OD,
在△OAC与△DBO中,
$\left\{\begin{array}{l}{AC=BO}\\{∠OAC=∠DBO}\\{OA=DB}\end{array}\right.$,
∴△OAC≌△DBO(SAS),
∴OC=OD,∠ODB=∠AOC,
∵AO⊥OC,
∴∠ODB=90°,
∵⊙O与BC相切,点C不是切点,
∴OC>半径,
∴OD>半径,
∴直线AB与⊙O的位置关系是相离.
点评 本题考查的是直线与圆的位置关系,解决此类问题可通过比较圆心到直线距离d与圆半径大小关系完成判定.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
18.在反比例函数y=$\frac{1-2m}{x}$的图象上有两点A(x1,y1)(x2,y2),当x2>x1>0时,有y2>y1,则m的取值范围是( )
| A. | m<0 | B. | m>0 | C. | m<$\frac{1}{2}$ | D. | m>$\frac{1}{2}$ |
2.峨边彝族自治县的总人口约有15.3万人,将15.3万人用科学记数法表示应为( )
| A. | 15.3×104人 | B. | 1.53×105人 | C. | 1.53×106人 | D. | 15.3×105人 |
19.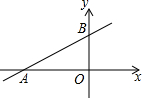 如图,直线y=kx+b交坐标轴于A(-3,0)、B(0,1)两点,则不等式-kx-b<0的解集为( )
如图,直线y=kx+b交坐标轴于A(-3,0)、B(0,1)两点,则不等式-kx-b<0的解集为( )
 如图,直线y=kx+b交坐标轴于A(-3,0)、B(0,1)两点,则不等式-kx-b<0的解集为( )
如图,直线y=kx+b交坐标轴于A(-3,0)、B(0,1)两点,则不等式-kx-b<0的解集为( )| A. | x>-3 | B. | x<-3 | C. | x>3 | D. | x<3 |
20.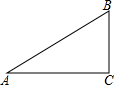 如图在Rt△ABC中,∠C=90°,AB=15,sinA=$\frac{1}{3}$,则BC等于( )
如图在Rt△ABC中,∠C=90°,AB=15,sinA=$\frac{1}{3}$,则BC等于( )
 如图在Rt△ABC中,∠C=90°,AB=15,sinA=$\frac{1}{3}$,则BC等于( )
如图在Rt△ABC中,∠C=90°,AB=15,sinA=$\frac{1}{3}$,则BC等于( )| A. | 45 | B. | 5 | C. | $\frac{1}{5}$ | D. | $\frac{1}{45}$ |