题目内容
11.过三点A(2,2),B(6,2),C(4,5)的圆的圆心坐标为( )| A. | (4,$\frac{17}{6}$) | B. | (4,3) | C. | (5,$\frac{17}{6}$) | D. | (5,3) |
分析 已知A(2,2),B(6,2),C(4,5),则过A、B、C三点的圆的圆心,就是弦的垂直平分线的交点,故求得AB的垂直平分线和BC的垂直平分线的交点即可.
解答 解:已知A(2,2),B(6,2),C(4,5),
∴AB的垂直平分线是x=$\frac{2+6}{2}$=4,
设直线BC的解析式为y=kx+b,
把B(6,2),C(4,5)代入上式得
$\left\{\begin{array}{l}{6k+b=2}\\{4k+b=5}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=-\frac{3}{2}}\\{b=11}\end{array}\right.$,
∴y=-$\frac{3}{2}$x+11,
设BC的垂直平分线为y=$\frac{2}{3}$x+m,
把线段BC的中点坐标(5,$\frac{7}{2}$)代入得m=$\frac{1}{6}$,
∴BC的垂直平分线是y=$\frac{2}{3}$x+$\frac{1}{6}$,
当x=4时,y=$\frac{17}{6}$,
∴过A、B、C三点的圆的圆心坐标为(4,$\frac{17}{6}$).
故选A.
点评 本题主要考查了待定系数法求一次函数的解析式,求两直线的交点,圆心是弦的垂直平分线的交点,理解圆心的作法是解决本题的关键.

练习册系列答案
相关题目
1.下列运算正确的是( )
| A. | 2x2-x2=1 | B. | 2x•3x=6x | C. | (-x)3÷(-x)2=-x | D. | (2x)-2=$\frac{1}{4}$x2 |
16.点A、B分别是函数y=$\frac{4}{x}$(x>0)和y=-$\frac{4}{x}$(x<0)图象上的一点,A、B两点的横坐标分别为a、b,且OA=OB,a+b≠0,则ab的值为( )
| A. | 2 | B. | -2 | C. | 4 | D. | -4 |
3.-5的倒数是( )
| A. | $\frac{1}{5}$ | B. | ±5 | C. | 5 | D. | -$\frac{1}{5}$ |
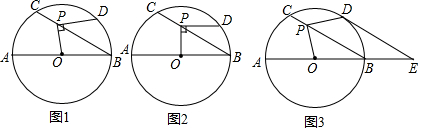
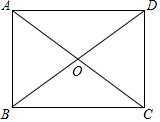 如图所示,已知平行四边形ABCD,对角线AC,BD相交于点O,∠OBC=∠OCB.
如图所示,已知平行四边形ABCD,对角线AC,BD相交于点O,∠OBC=∠OCB.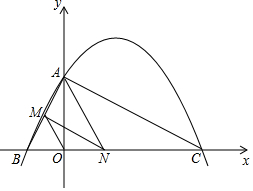 如图,已知二次函数y=ax2+bx+4的图象与x轴交于点B(-2,0),点C(8,0),与y轴交于点A.
如图,已知二次函数y=ax2+bx+4的图象与x轴交于点B(-2,0),点C(8,0),与y轴交于点A. 如图,小明为了测量一凉亭的高度AB(顶端A到水平地面BD的距离),在凉亭的旁边放置一个与凉亭台阶BC等高的台阶DE(DE=BC=0.5米,A、B、C三点共线),把一面镜子水平放置在平台上的点G处,测得CG=15米,然后沿直线CG后退到点E处,这时恰好在镜子里看到凉亭的顶端A,测得EG=3米,小明身高1.6米,则凉亭的高度AB约为( )
如图,小明为了测量一凉亭的高度AB(顶端A到水平地面BD的距离),在凉亭的旁边放置一个与凉亭台阶BC等高的台阶DE(DE=BC=0.5米,A、B、C三点共线),把一面镜子水平放置在平台上的点G处,测得CG=15米,然后沿直线CG后退到点E处,这时恰好在镜子里看到凉亭的顶端A,测得EG=3米,小明身高1.6米,则凉亭的高度AB约为( )