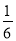题目内容
6.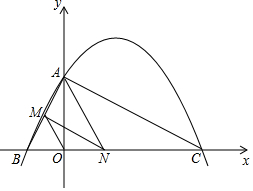 如图,已知二次函数y=ax2+bx+4的图象与x轴交于点B(-2,0),点C(8,0),与y轴交于点A.
如图,已知二次函数y=ax2+bx+4的图象与x轴交于点B(-2,0),点C(8,0),与y轴交于点A.(1)求二次函数y=ax2+bx+4的表达式;
(2)连接AC,AB,若点N在线段BC上运动(不与点B,C重合),过点N作NM∥AC,交AB于点M,当△AMN面积最大时,求N点的坐标;
(3)连接OM,在(2)的结论下,求OM与AC的数量关系.
分析 (1)由B、C的坐标,利用待定系数法可求得抛物线解析式;
(2)可设N(n,0),则可用n表示出△ABN的面积,由NM∥AC,可求得$\frac{AM}{AB}$,则可用n表示出△AMN的面积,再利用二次函数的性质可求得其面积最大时n的值,即可求得N点的坐标;
(3)由N点坐标可求得M点为AB的中点,由直角三角形的性质可得OM=$\frac{1}{2}$AB,在Rt△AOB和Rt△AOC中,可分别求得AB和AC的长,可求得AB与AC的关系,从而可得到OM和AC的数量关系.
解答 解:
(1)将点B,点C的坐标分别代入y=ax2+bx+4可得$\left\{\begin{array}{l}4a-2b+4=0\\ 64a+8b+4=0\end{array}\right.$,解得$\left\{\begin{array}{l}{a=-\frac{1}{4}}\\{b=\frac{3}{2}}\end{array}\right.$,
∴二次函数的表达式为y=-$\frac{1}{4}$x2+$\frac{3}{2}$x+4;
(2)设点N的坐标为(n,0)(-2<n<8),
则BN=n+2,CN=8-n.
∵B(-2,0),C(8,0),
∴BC=10,
在y=-$\frac{1}{4}$x2+$\frac{3}{2}$x+4中令x=0,可解得y=4,
∴点A(0,4),OA=4,
∴S△ABN=$\frac{1}{2}$BN•OA=$\frac{1}{2}$(n+2)×4=2(n+2),
∵MN∥AC,
∴$\frac{AM}{AB}=\frac{NC}{BC}=\frac{8-n}{10}$,
∴$\frac{{S}_{△AMN}}{{S}_{△ABN}}$=$\frac{AM}{AB}$=$\frac{8-n}{10}$,
∴${S_{△AMN}}=\frac{8-n}{10}{S_{△ABN}}=\frac{1}{5}(8-n)(n+2)=-\frac{1}{5}{(n-3)^2}+5$,
∵-$\frac{1}{5}$<0,
∴当n=3时,即N(3,0)时,△AMN的面积最大;
(3)当N(3,0)时,N为BC边中点,
∵MN∥AC,
∴M为AB边中点,
∴OM=$\frac{1}{2}$AB,
∵AB=$\sqrt{O{A}^{2}+O{B}^{2}}$=$\sqrt{16+4}$=2$\sqrt{5}$,AC=$\sqrt{O{C}^{2}+O{A}^{2}}$=$\sqrt{64+16}$=4$\sqrt{5}$,
∴AB=$\frac{1}{2}$AC,
∴OM=$\frac{1}{4}$AC.
点评 本题为二次函数的综合应用,涉及待定系数法、平行线分线段成比例、三角形的面积、二次函数的性质、直角三角形的性质、勾股定理等知识.在(1)中注意待定系数法的应用,在(2)中找到△AMN和△ABN的面积之间的关系是解题的关键,在(3)中确定出AB为OM和AC的中间“桥梁”是解题的关键.本题考查知识点较多,综合性较强,难度适中.

 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案 如图,直线a∥b,若∠1=40°,∠2=55°,则∠3的度数为( )
如图,直线a∥b,若∠1=40°,∠2=55°,则∠3的度数为( )| A. | 115° | B. | 105° | C. | 95° | D. | 85° |
| 地区 | A | B | C | D | E | F | G | H | I |
| 万册 | 28 | 24 | 23 | 14 | 16 | 15 | 5 |
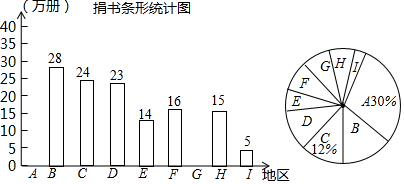
| A. | 捐书的总数为200万册 | |
| B. | 捐书数据的中位数是16万册 | |
| C. | 捐书数据的众数是60万册 | |
| D. | 捐书数扇形统计图中表示G的扇形的圆心角为30° |
| A. | (4,$\frac{17}{6}$) | B. | (4,3) | C. | (5,$\frac{17}{6}$) | D. | (5,3) |
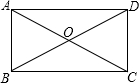 如图,矩形ABCD的对角线AC与BD相交于点O,∠ADB=30°,AB=4,则OC=( )
如图,矩形ABCD的对角线AC与BD相交于点O,∠ADB=30°,AB=4,则OC=( )| A. | 5 | B. | 4 | C. | 3.5 | D. | 3 |
 如图,在△ABC中,AC=BC,∠ACB=90°,⊙O(圆心O在△ABC内部)经过B、C两点,交AB于点E,过点E作⊙O的切线交AC于点F.延长CO交AB于点G,作ED∥AC交CG于点D
如图,在△ABC中,AC=BC,∠ACB=90°,⊙O(圆心O在△ABC内部)经过B、C两点,交AB于点E,过点E作⊙O的切线交AC于点F.延长CO交AB于点G,作ED∥AC交CG于点D 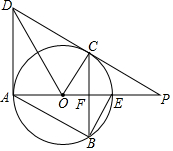 如图所示,直线DP和圆O相切于点C,交直径AE的延长线于点P.过点C作AE的垂线,交AE于点F,交圆O于点B.作平行四边形ABCD,连接BE,DO,CO.
如图所示,直线DP和圆O相切于点C,交直径AE的延长线于点P.过点C作AE的垂线,交AE于点F,交圆O于点B.作平行四边形ABCD,连接BE,DO,CO.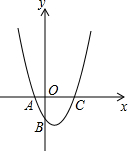 如图示二次函数y=ax2+bx+c的对称轴在y轴的右侧,其图象与x轴交于点A(-1,0)与点C(x2,0),且与y轴交于点B(0,-2),小强得到以下结论:①0<a<2;②-1<b<0;③c=-1;④当|a|=|b|时x2>$\sqrt{5}$-1;以上结论中正确结论的序号为①④.
如图示二次函数y=ax2+bx+c的对称轴在y轴的右侧,其图象与x轴交于点A(-1,0)与点C(x2,0),且与y轴交于点B(0,-2),小强得到以下结论:①0<a<2;②-1<b<0;③c=-1;④当|a|=|b|时x2>$\sqrt{5}$-1;以上结论中正确结论的序号为①④. B.
B.  C.
C. 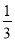 D.
D.