题目内容
13. 如图,△ABC中,∠B=90°,AB=11,BC=10,若⊙O的半径为5且与AB、BC相切,以下说法不正确的是①②③.
如图,△ABC中,∠B=90°,AB=11,BC=10,若⊙O的半径为5且与AB、BC相切,以下说法不正确的是①②③.①圆心O是∠B的角平分线与AC的交点;
②圆心O是∠B的角平分线与AB的垂直平分线的交点;
③圆心O是AB的垂直平分线与BC的垂直平分线的交点;
④圆心O是∠B的角平分线与BC的垂直平分线的交点.
分析 首先连接OD,OE,易得四边形ODBE是正方形,即可得点O在∠B的平分线上,OE是BC的垂直平分线,OD不是AB的垂直平分线,O不在AC的垂直平分线上,点O不在AC上.
解答 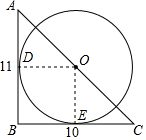 解:∵⊙O的半径为5且与AB、BC相切,
解:∵⊙O的半径为5且与AB、BC相切,
∴OD⊥AB,OE⊥BC,OD=OE=5,
∵∠B=90°,
∴四边形ODBE是正方形,
∴BE=BD=OE=OD=5,
∴点O在∠B的平分线上,CE=BC-BE=5,AD=AB-BD=11-5=6,
∴OE是BC的垂直平分线,OD不是AB的垂直平分线,
∵OA=$\sqrt{A{D}^{2}+O{D}^{2}}$=$\sqrt{61}$,OC=$\sqrt{O{E}^{2}+C{E}^{2}}$=5$\sqrt{2}$,
∴OA≠OC,
即O不在AC的垂直平分线上;
∵AC=$\sqrt{A{B}^{2}+B{C}^{2}}$=$\sqrt{221}$,
∴点O不在AC上.
∴①②③错误,④正确.
故答案为:①②③.
点评 此题考查了切线的性质、角平分线的性质以及线段垂直平分线的性质.注意证得四边形ODBE是正方形是关键.

练习册系列答案
相关题目
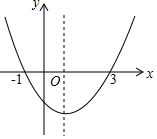 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论:
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论: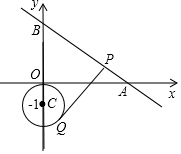 如图,直线y=-$\frac{3}{4}$x+3与x轴、y轴分别交于点A、B;点Q是以C(0,-2)为圆心、2为半径的圆上一动点,过Q点的切线交线段AB于点P,则线段PQ的最小值是2$\sqrt{3}$.
如图,直线y=-$\frac{3}{4}$x+3与x轴、y轴分别交于点A、B;点Q是以C(0,-2)为圆心、2为半径的圆上一动点,过Q点的切线交线段AB于点P,则线段PQ的最小值是2$\sqrt{3}$.