题目内容
12. 如图,AD、BC交于点O,EF过点O交AB于点E,交CD于点F,且AO=DO,BO=CO.求证:
如图,AD、BC交于点O,EF过点O交AB于点E,交CD于点F,且AO=DO,BO=CO.求证:(1)AB∥CD;
(2)EO=FO.
分析 (1)利用SAS证明△AOC≌△BOD证得∠A=∠B,即可;
(2)在△AOE和△OBF中.利用ASA证明全等,根据全等三角形的对应边相等即可证得.
解答 证明:(1)在△AOC和△BOD中,$\left\{\begin{array}{l}{AO=BO}\\{∠AOC=∠BOD}\\{CO=DO}\end{array}\right.$
∴△AOC≌△BOD,
∴∠A=∠B,
∴AB∥CD;
(2)在△AOE和△OBF中,$\left\{\begin{array}{l}{∠A=∠B}\\{AO=BO}\\{∠AOE=∠BOF}\end{array}\right.$,
∴△AOE≌△OBF.
∴OE=OF
点评 本题考查了全等三角形的判定与性质,正确理解证明三角形全等的条件是关键.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
1.抛物线y=2(x-3)2+1的顶点坐标是( )
| A. | (3,1) | B. | (4,-1) | C. | (-3,1) | D. | (-3,-1) |
7.下列说法错误的是( )
| A. | a2与(-a)2相等 | B. | $\sqrt{{a}^{2}}$与$\sqrt{(-a)^{2}}$互为相反数 | ||
| C. | $\root{3}{a}$与$\root{3}{-a}$是互为相反数 | D. | -|a|与|-a|互为相反数 |
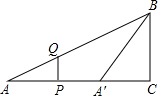 如图,在Rt△ABC中,∠C=90°,AC=4,BC=2,P、Q分别是AC、AB边上的动点,PQ∥BC,点A关于直线PQ的对称点为A′,连结A′B,设线段AP的长为t.
如图,在Rt△ABC中,∠C=90°,AC=4,BC=2,P、Q分别是AC、AB边上的动点,PQ∥BC,点A关于直线PQ的对称点为A′,连结A′B,设线段AP的长为t.