题目内容
3. 如图,正六边形ABCDEF的边长为2,则对角线AF=2$\sqrt{3}$.
如图,正六边形ABCDEF的边长为2,则对角线AF=2$\sqrt{3}$.
分析 作BG⊥AF,垂足为G.构造等腰三角形ABF,在直角三角形ABG中,求出AG的长,即可得出AF.
解答 解:作BG⊥AF,垂足为G.如图所示:
∵AB=BF=2,
∴AG=FG,
∵∠ABF=120°,
∴∠BAF=30°,
∴AG=AB•cos30°=2×$\frac{\sqrt{3}}{2}$=$\sqrt{3}$,
∴AC=2AG=2$\sqrt{3}$;
故答案为2$\sqrt{3}$.
点评 本题考查了正多边形和圆、正六边形的性质、等腰三角形的性质、三角函数;熟练掌握正六边形的性质,由三角函数求出AG是解决问题的关键.

练习册系列答案
相关题目
11.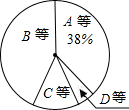 某校为了解七年级男生体操测试情况,随机抽取了50名男生的测试成绩进行统计,根据评分标准,将他们的成绩分为A,B,C,D四个等级,并绘制成频数分布表和扇形统计图(如图).
某校为了解七年级男生体操测试情况,随机抽取了50名男生的测试成绩进行统计,根据评分标准,将他们的成绩分为A,B,C,D四个等级,并绘制成频数分布表和扇形统计图(如图).
(1)在被调查的男生中,成绩为B等级的有23人,占被调查男生人数的46%,m=0.38;
(2)求a,b,n的值;
(3)如果该校七年级共有200名男生,试估计这200名男生中成绩达到A等级和B等级的共有多少人.
 某校为了解七年级男生体操测试情况,随机抽取了50名男生的测试成绩进行统计,根据评分标准,将他们的成绩分为A,B,C,D四个等级,并绘制成频数分布表和扇形统计图(如图).
某校为了解七年级男生体操测试情况,随机抽取了50名男生的测试成绩进行统计,根据评分标准,将他们的成绩分为A,B,C,D四个等级,并绘制成频数分布表和扇形统计图(如图).| 等级 | 成绩x/分 | 频数/(人数) | 频率 |
| A | 9.0≤x≤10.0 | a | m |
| B | 7.0≤x<9.0 | 23 | 0.46 |
| C | 6.0≤x<7.0 | b | n |
| D | 0.0≤x<6.0 | 3 | 0.06 |
| 合计 | 50 | 1.00 |
(2)求a,b,n的值;
(3)如果该校七年级共有200名男生,试估计这200名男生中成绩达到A等级和B等级的共有多少人.
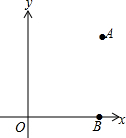 如图,在平面直角坐标系xOy中点A(6,8),点B(6,0).
如图,在平面直角坐标系xOy中点A(6,8),点B(6,0). 如图,在平面直角坐标系中,矩形ABCD的边DA与y轴正半轴重合,D与原点重合.且AD=2,AB=1,以DB为对称轴,将Rt△ADB翻折,点A落在点E处,过E点作EM⊥x轴,垂足是M,另有一点F与点B关于原点对称.
如图,在平面直角坐标系中,矩形ABCD的边DA与y轴正半轴重合,D与原点重合.且AD=2,AB=1,以DB为对称轴,将Rt△ADB翻折,点A落在点E处,过E点作EM⊥x轴,垂足是M,另有一点F与点B关于原点对称.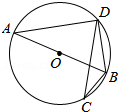 如图所示,已知⊙O是△ABD的外接圆,AB是⊙O的直径,CD是⊙O的弦,∠ABD=54°,则∠BCD=36°.
如图所示,已知⊙O是△ABD的外接圆,AB是⊙O的直径,CD是⊙O的弦,∠ABD=54°,则∠BCD=36°.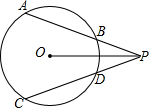 如图,已知过P点的两条直线交⊙O于A,B,C,D四点,且OP平分∠APC.
如图,已知过P点的两条直线交⊙O于A,B,C,D四点,且OP平分∠APC.