题目内容
19．一个三角形某一边长是4cm，且它的面积小于8，则此边上的高h的取值范围是（ ）| A． | h＜8 | B． | h＞0 | C． | 4＜h＜8 | D． | 0＜h＜4 |
分析 利用三角形面积S为8cm2，得出x的值，进而得出S小于cm2时x的取值范围．
解答 解：根据题意得$\frac{1}{2}$×4•h＜8，
解得：h＜4，
∴此边上的高h的取值范围是：0＜h＜4，
故选D．
点评 本题考查了三角形的面积，解不等式，正确的求出不等式的解集是解题的关键．
练习册系列答案
相关题目
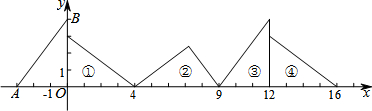
9．
星期天，小王五朋友家借书，如图是他离家的距离y（千米）与时间x（分钟）的关系图象．根据图象信息，下列说法正确的是（ ）
星期天，小王五朋友家借书，如图是他离家的距离y（千米）与时间x（分钟）的关系图象．根据图象信息，下列说法正确的是（ ）| A． | 小王去时的速度大于回家的速度 | |
| B． | 小王在朋友家停留了10分钟 | |
| C． | 小王去时花的时间少于回家时所花的时间 | |
| D． | 小王去时走下坡路，回家时走上坡路 |
10．
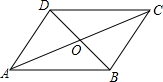如图，在?ABCD中，AD=5，AC=10，BD=6，则△BOC的周长为（ ）
如图，在?ABCD中，AD=5，AC=10，BD=6，则△BOC的周长为（ ）| A． | 13 | B． | 16 | C． | 18 | D． | 21 |
7．广东某县生产柚子，其中A村有柚子200吨，B村有柚子280吨，先将这些柚子运到C、D两个仓库．已知C仓库可存储260吨，D仓库可存储220吨，从A村运往C、D两处的费用分别为每吨20元和25元；从B村运往C、D两仓库的费用分别为每吨16元和20元．设从A村运往C仓库的柚子重量为x吨，A、B两村运往两仓库的柚子运输费用分别为yA元，yB元．
（1）请填写下表，并求出yA，yB与x之间的函数关系式．
（2）考虑到B村的经济承受能力，B村的柚子运费不得超过4800元，在这种情况下，请问怎样调运，才能使两村运费之和最小？最小是多少？求出这个最小值．
（1）请填写下表，并求出yA，yB与x之间的函数关系式．
| C | D | 总计 | |
| A | x吨 | 200-x | 200吨 |
| B | 260-x | x+20 | 280吨 |
| 总计 | 260吨 | 220吨 | 480吨 |
11．若关于x的不等式mx-n＞0的解集是x＜$\frac{1}{4}$，则关于x的不等式（n-m）x＞（m+n）的解集是（ ）
| A． | x＜-$\frac{5}{3}$ | B． | x＞-$\frac{5}{3}$ | C． | x＜$\frac{5}{3}$ | D． | x＞$\frac{5}{3}$ |