题目内容
平面内有四个点A、B、C、D,其中∠ABC=1500,∠ADC=300,AB=BC=1,则满足题意的BD长
 的最大值是 。
的最大值是 。
 。
。
【考点】圆周角定理,圆内接四边形的性质,等腰三角形的性质,勾股定理,二次根式化简。
【分析】如图,考虑到∠ABC=1500,∠ADC=300,根据圆内 接四边形对角互补的性质,知点A、B、C、D在同一圆上,且点D在优弧AC上,所以BD长
接四边形对角互补的性质,知点A、B、C、D在同一圆上,且点D在优弧AC上,所以BD长 的最大值是BO的延长线与⊙O的交点(点O是AB和BC中垂线的交点)。
的最大值是BO的延长线与⊙O的交点(点O是AB和BC中垂线的交点)。
连接OC,过点C作CH⊥BD于点H ,
,

设OC=x,

在Rt△CHD中,由勾股定理,得 ,
,
∴ 。
。
∴ 。
。
∴BD长 的最大值是
的最大值是 。
。

练习册系列答案
相关题目

 的图象与正比例函数
的图象与正比例函数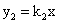
 的图象交于点(2,1),则使y1>y2的x的取值范围是【 】
的图象交于点(2,1),则使y1>y2的x的取值范围是【 】

 ,AC=
,AC= ,BC=6,点M在AB边上,且AM=
,BC=6,点M在AB边上,且AM= BM,在线段AC上取点N,使△AMN与△ABC相似,求线段MN的长。
BM,在线段AC上取点N,使△AMN与△ABC相似,求线段MN的长。
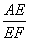
 =3,求
=3,求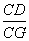
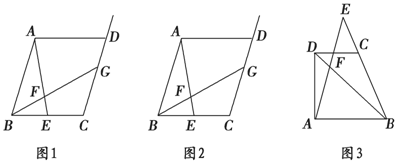

 :
: 的值是________(用含有m的代数式表示),试写出解答过程.
的值是________(用含有m的代数式表示),试写出解答过程.

 cm2.
cm2.
 在Rt△ABC中,∠C=900,∠B=300,BC=
在Rt△ABC中,∠C=900,∠B=300,BC=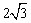 ,点D是BC边上一动点(不与点B、C重合),过点D作DE⊥BC交AB边于点E,将∠B沿直
,点D是BC边上一动点(不与点B、C重合),过点D作DE⊥BC交AB边于点E,将∠B沿直 线DE翻折,点B落在射线BC上的点F处,当△AEF为等腰三角形时,BD的长为 。
线DE翻折,点B落在射线BC上的点F处,当△AEF为等腰三角形时,BD的长为 。
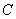
 :
:
 的顶点在坐标轴上.
的顶点在坐标轴上.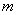
 的值;
的值;
 时,抛物线
时,抛物线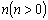
 个单位后与抛物线
个单位后与抛物线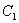
 :
: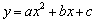
 关于
关于
 轴对称,且
轴对称,且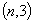
 ,求
,求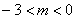
 时,抛物线
时,抛物线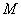
 ,且过点
,且过点
 .问在直线
.问在直线
 上是否存在一点
上是否存在一点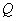
 使得△
使得△
 的周长最小,如果存在,求出点
的周长最小,如果存在,求出点 AB′C′的位置,B,A,C′三点共线,则线段BC扫过的区域面积为 .
AB′C′的位置,B,A,C′三点共线,则线段BC扫过的区域面积为 .
 8cm,BC=4cm,D、E分别为边AB、BC的中点
8cm,BC=4cm,D、E分别为边AB、BC的中点 ,连结DE,点P从点A出发,沿折线AD-DE-EB运动,到点B停止.点P在AD上以
,连结DE,点P从点A出发,沿折线AD-DE-EB运动,到点B停止.点P在AD上以
 cm/s的速度运动,在折线DE-EB上以1cm/s的速度运动.当点P与点A不重合时,过点P作PQ⊥AC于点Q,以PQ为边作正方形PQMN,使点M落在线段AC上.设点P的运动时间为t(s).
cm/s的速度运动,在折线DE-EB上以1cm/s的速度运动.当点P与点A不重合时,过点P作PQ⊥AC于点Q,以PQ为边作正方形PQMN,使点M落在线段AC上.设点P的运动时间为t(s). 长为______cm,(用含t的代数式表示).
长为______cm,(用含t的代数式表示). 度沿M-N-M连续做往返运动,直至点P与点E重合时,点H停止往返运动;当点P在线段EB上运动时,点H始终在线段MN的中心处.直接写出在点P的整个运动过程中,点H落在线段CD上时t的取值范围.
度沿M-N-M连续做往返运动,直至点P与点E重合时,点H停止往返运动;当点P在线段EB上运动时,点H始终在线段MN的中心处.直接写出在点P的整个运动过程中,点H落在线段CD上时t的取值范围.