题目内容
12.化简求值:(1)$\frac{4{a}^{2}-8ab+4{b}^{2}}{2{a}^{2}-2{b}^{2}}$,其中a=2,b=3.
(2)$\frac{{x}^{2}-4y}{4{x}^{2}-8xy}$,其中x=$\frac{1}{2}$,y=$\frac{1}{4}$.
分析 (1)首先把分子和分母分解因式,约分,然后代入数值计算即可;
(2)首先把分子、分母分解因式,然后代入数值计算.
解答 解:(1)原式$\frac{4(a-b)^{2}}{2(a+b)(a-b)}$=$\frac{2(a-b)}{a+b}$,
当a=2,b=3时,原式=$\frac{2×(2-3)}{2+3}$=-$\frac{2}{5}$;
(2)原式=$\frac{{x}^{2}-4y}{4x(x-2y)}$,
当x=$\frac{1}{2}$,y=$\frac{1}{4}$时,4x(x-2y)=4×$\frac{1}{2}$($\frac{1}{2}$-2×$\frac{1}{2}$)=0,则分式没有意义.
点评 本题考查了分式的化简求值,分式化简关键是把分子、分母因式分解.

练习册系列答案
相关题目
 如图,在△ABC中,∠ACB=90°,AC=6cm,BC=8cm.
如图,在△ABC中,∠ACB=90°,AC=6cm,BC=8cm.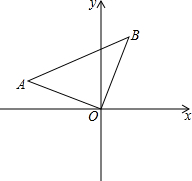 如图,△A0B中,∠A0B=90°,AO=BO,点B的坐标为(2,5).
如图,△A0B中,∠A0B=90°,AO=BO,点B的坐标为(2,5). 如图,△ABC中,点D在BC上,EF∥BC,分别交AB,AC,AD于点E,F,G,图中共有几对相似三角形?分别是哪几对?
如图,△ABC中,点D在BC上,EF∥BC,分别交AB,AC,AD于点E,F,G,图中共有几对相似三角形?分别是哪几对?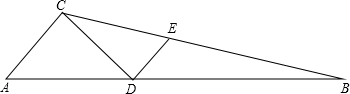 如图,在ABC中,已知D为AB边上一点,AC⊥CD,DE⊥CD,CD:CE=4:5,S△ACD:S△CDB=2:3,则tanA=$\frac{4}{5}$.
如图,在ABC中,已知D为AB边上一点,AC⊥CD,DE⊥CD,CD:CE=4:5,S△ACD:S△CDB=2:3,则tanA=$\frac{4}{5}$.