Question

20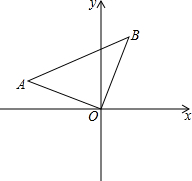．如图，△A0B中，∠A0B=90°，AO=BO，点B的坐标为（2，5）．
（1）求出点A的坐标；
（2）画出△AOB关于x轴对称的△A′0B′，并写出点A′、B′的坐标．

Answer 1

分析 （1）过点A作AC⊥x轴于点C，过点B作BD⊥x轴于点D，再由AAS定理得出△AOC≌△OBD，故可得出AC及OC的长，由此可得出结论；
（2）作点AB关于x轴的对称点A′、B′，连接OA′与OB′，并写出各点坐标即可．

解答 解：（1）过点A作AC⊥x轴于点C，过点B作BD⊥x轴于点D，
∵∠AOB=90°，
∴∠AOC+∠BOD=90°，
∵∠AOC+∠OAC=90°，
∴∠BOD=∠OAC．
在△AOC与△OBD中，
$\left\{\begin{array}{l}∠OAC=∠BOD\\∠ACO=∠ODB\\ OA=OB\end{array}\right.$，
∴△AOC≌△OBD（AAS）．
∵点B的坐标为（2，5），
∴OD=AC=2，OC=BD=5，
∴A（-5，2）；

（2）如图所示，A′（-5，-2），B′（2，-5）．

点评 本题考查的是作图-轴对称变换，熟知关于x轴对称的点的坐标特点是解答此题的关键．