题目内容
2.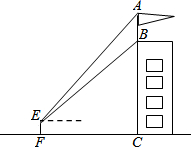 如图,某建筑物BC上有一旗杆AB,小刘在与BC相距24m的F处,由E点观测到旗杆顶部A的仰角为52°、底部B的仰角为45°,小刘的观测点与地面的距离EF为1.6m.
如图,某建筑物BC上有一旗杆AB,小刘在与BC相距24m的F处,由E点观测到旗杆顶部A的仰角为52°、底部B的仰角为45°,小刘的观测点与地面的距离EF为1.6m.(1)求建筑物BC的高度;
(2)求旗杆AB的高度.
(结果精确到0.1m.参考数据:$\sqrt{2}$≈1.41,sin52°≈0.79,tan52°≈1.28)
分析 (1)先过点E作ED⊥BC于D,由已知底部B的仰角为45°得BD=ED=FC=24m,DC=EF=1.6m,从而求出BC.
(2)由已知由E点观测到旗杆顶部A的仰角为52°可求出AD,则AB=AD-BD.
解答  解:(1)过点E作ED⊥BC于D,
解:(1)过点E作ED⊥BC于D,
根据题意得:EF⊥FC,ED∥FC,
∴四边形CDEF是矩形,
已知底部B的仰角为45°即∠BED=45°,
∴∠EBD=45°,
∴BD=ED=FC=24m,
∴BC=BD+DC=BD+EF=12+1.6=25.6(m),
答:建筑物BC的高度为25.6m.
(2)已知由E点观测到旗杆顶部A的仰角为52°,即∠AED=52°,
∴AD=ED•tan52°
≈24×1.28≈30.8,
∴AB=AD-BD=30.8-24=6.8.
答:旗杆AB的高度约为6.8m.
点评 此题考查的知识点是解直角三角形的应用,解题的关键是把实际问题转化为解直角三角形问题,先得到等腰直角三角形,再根据三角函数求解.

练习册系列答案
相关题目
12.某服装店原计划按每套200元的价格销售一批保暖内衣,但上市后销售不佳,为减少库存积压,两次连续降价打折处理,最后价格调整为每套128元.若两次降价折扣率相同,则每次降价率为( )
| A. | 8% | B. | 18% | C. | 20% | D. | 25% |
14.如果一组数据:6,-2,0,6,4,x的平均数是2,那么x等于( )
| A. | 3 | B. | 4 | C. | -2 | D. | 6 |
11.不等式-2x-1≥1的解集是( )
| A. | x≥-1 | B. | x≤-1 | C. | x≤0 | D. | x≤1 |
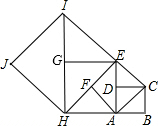 如图,如果以正方形ABCD的对角线AC为边作第二个正方形ACEF,再以对角线AE为边作第三个正方形AEGH,如此下去…,已知正方形ABCD的面积S1为1,按上述方法所作的正方形的面积依次为S2,S3,…,Sn(n为正整数),那么第2015个正方形的面积S2015为22014.
如图,如果以正方形ABCD的对角线AC为边作第二个正方形ACEF,再以对角线AE为边作第三个正方形AEGH,如此下去…,已知正方形ABCD的面积S1为1,按上述方法所作的正方形的面积依次为S2,S3,…,Sn(n为正整数),那么第2015个正方形的面积S2015为22014.