题目内容
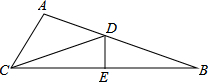 已知在△ABC中,∠ACB=60°,AC=2,BC=6,将△ABC沿着DE翻折,使点B与点C重合,折痕DE交AB于点D,交BC于点E,那么△ACD的面积为
已知在△ABC中,∠ACB=60°,AC=2,BC=6,将△ABC沿着DE翻折,使点B与点C重合,折痕DE交AB于点D,交BC于点E,那么△ACD的面积为考点:翻折变换(折叠问题)
专题:
分析:作AF垂直于BC于点F,利用RT△AFC易得CF=1,AF=
,由对折性可得BE=CE,BD=CD,AF∥DE,求出BE和BF,利用比例式求出DE,再运用S△ACD=S△ABC-S△DCB即可得出答案.
| 3 |
解答:解:如图,作AF垂直于BC于点F,

∵∠ACB=60°,AC=2,
∴CF=1,AF=
,
由对折性可得BE=CE,BD=CD,∠DEB=∠DEC=90°,
∴AF∥DE,
∵BC=6,
∴BE=CE=3,
∴BF=BE+EF=3+2=5,
∴
=
,即
=
,解得DE=
.
∴S△ACD=S△ABC-S△DCB=
BC•AF-
BC•DE=
×6×
-
×6×
=
.
故答案为:
.

∵∠ACB=60°,AC=2,
∴CF=1,AF=
| 3 |
由对折性可得BE=CE,BD=CD,∠DEB=∠DEC=90°,
∴AF∥DE,
∵BC=6,
∴BE=CE=3,
∴BF=BE+EF=3+2=5,
∴
| DE |
| AF |
| BE |
| BF |
| DE | ||
|
| 3 |
| 5 |
| 3 |
| 5 |
| 3 |
∴S△ACD=S△ABC-S△DCB=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 1 |
| 2 |
| 3 |
| 5 |
| 3 |
6
| ||
| 5 |
故答案为:
6
| ||
| 5 |
点评:本题主要考查了翻折变换,解题的关键是明确图形的形状和大小不变,位置变化,对应边和对应角相等.

练习册系列答案
相关题目
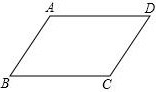 已知:如图,在四边形ABCD中,AB∥CD,∠B=∠D.求证:AD∥BC(用两种不同的方法证明)
已知:如图,在四边形ABCD中,AB∥CD,∠B=∠D.求证:AD∥BC(用两种不同的方法证明) 如图,正方形OABC中顶点B在一双曲线上,请在图中画出一条过点B的直线,使之与双曲线的另一支交于点D,且满足线段BD最短.
如图,正方形OABC中顶点B在一双曲线上,请在图中画出一条过点B的直线,使之与双曲线的另一支交于点D,且满足线段BD最短. 如图,两同心圆的圆心为A,大圆的弦AB切小圆于P,两圆的半径分别为2和1.若用阴影部分围成一个圆锥,则该圆锥的底面半径为
如图,两同心圆的圆心为A,大圆的弦AB切小圆于P,两圆的半径分别为2和1.若用阴影部分围成一个圆锥,则该圆锥的底面半径为 实数x在数轴上的位置如图所示,则化简
实数x在数轴上的位置如图所示,则化简