题目内容
 一辆园林喷灌车和一辆公交车分别从一条笔直公路两端点A、B同时出发匀速行驶,喷灌车中途停车在供水站加满水后继续以原速进行作业到达终点B,公交车到达A处进站检修,之后沿原路原点返回到点B.如图是两车与点A的距离y(千米)与运行时间t(时)的函数图象.
一辆园林喷灌车和一辆公交车分别从一条笔直公路两端点A、B同时出发匀速行驶,喷灌车中途停车在供水站加满水后继续以原速进行作业到达终点B,公交车到达A处进站检修,之后沿原路原点返回到点B.如图是两车与点A的距离y(千米)与运行时间t(时)的函数图象.(1)分别求出喷灌车与公交车的速度;
(2)求两辆车在途中相遇的时间;
(3)当两车之间距离小于1千米时,求t的取值范围.
考点:一次函数的应用
专题:
分析:(1)喷灌车是0.8小时行驶了10千米,公交车是0.8小时行驶了20千米.由速度=路程÷时间进行计算;
(2)根据两车速度之和×时间=路程进行计算;
(3)分三段:相向而行、喷灌车停止,公交车行驶、同向而行.
(2)根据两车速度之和×时间=路程进行计算;
(3)分三段:相向而行、喷灌车停止,公交车行驶、同向而行.
解答: 解:(1)喷灌车的速度是:10÷1=10(千米/小时).
解:(1)喷灌车的速度是:10÷1=10(千米/小时).
公交车的速度是:20÷0.8=25(千米/小时).
(2)喷灌车中途加水的时间是:2.6-1-1=0.6(小时)
设两辆车在途中相遇的第一次时间是两车出发后t小时,则
(10+25)t=20,
解得 t=
.
根据图示知,第二次相遇的时间是0.6+1=1.6(小时)
答:两辆车在途中相遇的时间是两车出发
小时或2.8小时;
(3)当两车相向而行时,19<(10+25)t<20.
解得
<t<
.
当喷灌车停止,公交车从A到B的过程中,9<25×(t-1.2)<10,
解得
<t<
.
当两车同向而行时,(25-10)(t-1.6)<1,且t>1.6
解得
<t<
.
综上所述,当两车之间距离小于1千米时,t的取值范围是:
<t<
或
<t<
或
<t<
.
 解:(1)喷灌车的速度是:10÷1=10(千米/小时).
解:(1)喷灌车的速度是:10÷1=10(千米/小时).公交车的速度是:20÷0.8=25(千米/小时).
(2)喷灌车中途加水的时间是:2.6-1-1=0.6(小时)
设两辆车在途中相遇的第一次时间是两车出发后t小时,则
(10+25)t=20,
解得 t=
| 4 |
| 7 |
根据图示知,第二次相遇的时间是0.6+1=1.6(小时)
答:两辆车在途中相遇的时间是两车出发
| 4 |
| 7 |
(3)当两车相向而行时,19<(10+25)t<20.
解得
| 19 |
| 35 |
| 4 |
| 7 |
当喷灌车停止,公交车从A到B的过程中,9<25×(t-1.2)<10,
解得
| 39 |
| 25 |
| 8 |
| 5 |
当两车同向而行时,(25-10)(t-1.6)<1,且t>1.6
解得
| 8 |
| 5 |
| 5 |
| 3 |
综上所述,当两车之间距离小于1千米时,t的取值范围是:
| 19 |
| 35 |
| 4 |
| 7 |
| 39 |
| 25 |
| 8 |
| 5 |
| 8 |
| 5 |
| 5 |
| 3 |
点评:本题考查了一次函数综合题.解题时,需要学生具备一定的读图能力.

练习册系列答案
相关题目
若a<b,则下列不等式一定成立的是( )
| A、a-2>b-2 | ||||
B、
| ||||
| C、-b>-a | ||||
| D、a-b<0 |
已知y=kx+b,当x=0时,y=2;当x=2时,y=0,则当x=-2时,y等于( )
| A、-2 | B、0 | C、2 | D、4 |
 一天,小明不小心将手电筒上的圆形玻璃片打碎了,碎片中有一块如图所示,小明想去玻璃店重新配一块;
一天,小明不小心将手电筒上的圆形玻璃片打碎了,碎片中有一块如图所示,小明想去玻璃店重新配一块;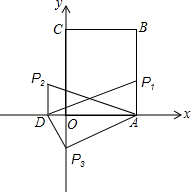 如图所示平面直角坐标系中,矩形OABC的顶点B的坐标为(4,8),若一次函数y=kx+2的图象平分矩形OABC的面积.
如图所示平面直角坐标系中,矩形OABC的顶点B的坐标为(4,8),若一次函数y=kx+2的图象平分矩形OABC的面积. 如图,某校7年级的学生从学校O点出发,要到某地P处进行探险活动,他们先向正西方向走8km到A处,又往正南方向走4km到B处,又折向正东方向走6km到C处,再折向正北方向走8km到D处,最后又往正东方向走4km才到探险地P;取点O为原点,取点O的正东方向为x轴的正方向,取点O的正北方向为y轴的正方向,以2km为一个单位长度建立平面直角坐标系.
如图,某校7年级的学生从学校O点出发,要到某地P处进行探险活动,他们先向正西方向走8km到A处,又往正南方向走4km到B处,又折向正东方向走6km到C处,再折向正北方向走8km到D处,最后又往正东方向走4km才到探险地P;取点O为原点,取点O的正东方向为x轴的正方向,取点O的正北方向为y轴的正方向,以2km为一个单位长度建立平面直角坐标系.