题目内容
10.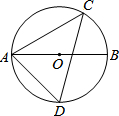 如图,AB为⊙O的直径,点C在⊙O上,且∠CAB=30°,点D为弧AB的中点,AC=4$\sqrt{3}$.求CD的长.
如图,AB为⊙O的直径,点C在⊙O上,且∠CAB=30°,点D为弧AB的中点,AC=4$\sqrt{3}$.求CD的长.
分析 作AE⊥CD于E,连接BD,根据圆周角定理得到∠ACD=45°,∠ADB=90°,∠CDB=∠CAB=30°,根据正弦和正切的定义计算即可.
解答 解:作AE⊥CD于E,连接BD,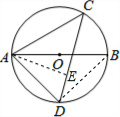
∵点D为弧AB的中点,
∴∠ACD=45°,
∴AE=CE=AC×$\frac{\sqrt{2}}{2}$=2$\sqrt{6}$,
由圆周角定理得,∠ADB=90°,∠CDB=∠CAB=30°,
∴∠ADC=60°,
∴DE=$\frac{AE}{tan∠ADC}$=2$\sqrt{2}$,
∴CD=DE+CE=2$\sqrt{6}$+2$\sqrt{2}$.
点评 本题考查的是圆周角定理的应用和锐角三角函数的定义,掌握在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半、半圆(或直径)所对的圆周角是直角是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
8. 如图,已知AC与BD相交于点O,OE是∠AOD的平分线,可以作为假命题“相等的角是对顶角”的反例的是( )
如图,已知AC与BD相交于点O,OE是∠AOD的平分线,可以作为假命题“相等的角是对顶角”的反例的是( )
 如图,已知AC与BD相交于点O,OE是∠AOD的平分线,可以作为假命题“相等的角是对顶角”的反例的是( )
如图,已知AC与BD相交于点O,OE是∠AOD的平分线,可以作为假命题“相等的角是对顶角”的反例的是( )| A. | ∠AOB=∠DOC | B. | ∠EOC<∠DOC | C. | ∠EOB=∠EOC | D. | ∠EOC>∠DOC |
9.对于双曲线y=$\frac{1-m}{x}$,当x>0时,y随x的增大而减小,则m的取值范围为( )
| A. | m>0 | B. | m>1 | C. | m<0 | D. | m<1 |
6. 如图,在平面直角坐标系中,边长为1的正方形ABCD中,AD边的中点处有一动点P,动点P沿P→D→C→B→A→P运动一周,则P点的纵坐标y与点P走过的路程s之间的函数关系用图象表示大致是( )
如图,在平面直角坐标系中,边长为1的正方形ABCD中,AD边的中点处有一动点P,动点P沿P→D→C→B→A→P运动一周,则P点的纵坐标y与点P走过的路程s之间的函数关系用图象表示大致是( )
 如图,在平面直角坐标系中,边长为1的正方形ABCD中,AD边的中点处有一动点P,动点P沿P→D→C→B→A→P运动一周,则P点的纵坐标y与点P走过的路程s之间的函数关系用图象表示大致是( )
如图,在平面直角坐标系中,边长为1的正方形ABCD中,AD边的中点处有一动点P,动点P沿P→D→C→B→A→P运动一周,则P点的纵坐标y与点P走过的路程s之间的函数关系用图象表示大致是( )| A. | 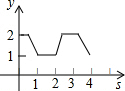 | B. | 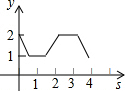 | C. | 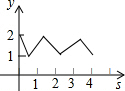 | D. | 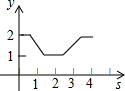 |
20.某校抽取10名学生参加“心理健康”知识测试,他们得分情况如表:
那么这10名学生所得分数的众数和中位数分别是( )
| 分数 | 80 | 85 | 90 | 85 |
| 人数 | 2 | 3 | 4 | 1 |
| A. | 95和85 | B. | 90和85 | C. | 90和87.5 | D. | 85和87.5 |
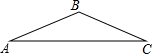 如图,一座厂房屋顶人字架的跨度AC=12m,上弦AB=BC,∠BAC=25°.若用科学计算器求上弦AB的长,则下列按键顺序正确的是( )
如图,一座厂房屋顶人字架的跨度AC=12m,上弦AB=BC,∠BAC=25°.若用科学计算器求上弦AB的长,则下列按键顺序正确的是( )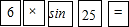



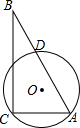 如图,直角△ABC的直角顶点C,另一顶点A及斜边AB的中点D都在⊙O上,已知:AC=6,BC=8,则⊙O的半径为$\frac{25}{8}$.
如图,直角△ABC的直角顶点C,另一顶点A及斜边AB的中点D都在⊙O上,已知:AC=6,BC=8,则⊙O的半径为$\frac{25}{8}$.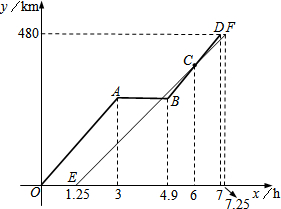 “十•一”长假,小王与小叶相约分别驾车从南京出发,沿同一路线驶往距南京480km的甲地旅游.小王由于有事临时耽搁,比小叶迟出发1.25小时.而小叶的汽车中途发生故障,等排除故障后,立即加速赶往甲地.若从小叶出发开始计时,图中的折线O-A-B-D、线段EF分别表示小叶、小王两人与南京的距离y1(km)、y2(km)与时间x(h)之间的函数关系.
“十•一”长假,小王与小叶相约分别驾车从南京出发,沿同一路线驶往距南京480km的甲地旅游.小王由于有事临时耽搁,比小叶迟出发1.25小时.而小叶的汽车中途发生故障,等排除故障后,立即加速赶往甲地.若从小叶出发开始计时,图中的折线O-A-B-D、线段EF分别表示小叶、小王两人与南京的距离y1(km)、y2(km)与时间x(h)之间的函数关系.