题目内容
4. 在一个长为2米,宽为1米的矩形草地上,如图堆放着一根长方体的木块,它的棱长和场地宽AD平行且>AD,木块的正视图是边长为0.2米的正方形,一只蚂蚁从点A处,到达C处需要走的最短路程是2.6米.
在一个长为2米,宽为1米的矩形草地上,如图堆放着一根长方体的木块,它的棱长和场地宽AD平行且>AD,木块的正视图是边长为0.2米的正方形,一只蚂蚁从点A处,到达C处需要走的最短路程是2.6米.
分析 解答此题要将木块展开,然后根据两点之间线段最短解答.
解答 解:由题意可知,将木块展开, 相当于是AB+2个正方形的宽,
相当于是AB+2个正方形的宽,
∴长为2+0.2×2=2.4米;宽为1米.
于是最短路径为:$\sqrt{2.{4}^{2}+{1}^{2}}$=2.6米.
故答案为:2.6
点评 本题主要考查两点之间线段最短,有一定的难度,要注意培养空间想象能力.

练习册系列答案
相关题目
19.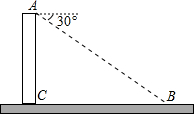 如图,为了测量楼的高度,自楼的顶部A看地面上的一点B,俯角为30°,已知地面上的这点与楼的水平距离BC为30m,那么楼的高度AC为( )
如图,为了测量楼的高度,自楼的顶部A看地面上的一点B,俯角为30°,已知地面上的这点与楼的水平距离BC为30m,那么楼的高度AC为( )
 如图,为了测量楼的高度,自楼的顶部A看地面上的一点B,俯角为30°,已知地面上的这点与楼的水平距离BC为30m,那么楼的高度AC为( )
如图,为了测量楼的高度,自楼的顶部A看地面上的一点B,俯角为30°,已知地面上的这点与楼的水平距离BC为30m,那么楼的高度AC为( )| A. | 15m | B. | 20m | C. | 10$\sqrt{3}$m | D. | 20$\sqrt{3}$m |
16.若数轴上的点M对应的点是-2,那么与M相距1个单位长度的点N所对应的数是( )
| A. | 1 | B. | -1 | C. | -1或-3 | D. | -1或3 |
14.已知a>0,b<0,且a的绝对值小于b的绝对值,则直线y=ax+b和直线y=bx+a相交于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
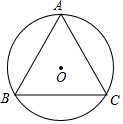 如图,等边△ABC内接于⊙O,已知⊙O的半径为4,则边长BC的长为4$\sqrt{3}$.
如图,等边△ABC内接于⊙O,已知⊙O的半径为4,则边长BC的长为4$\sqrt{3}$. 画出如图几何体的三视图.
画出如图几何体的三视图.