题目内容
7.如图,将边长为12的正方形ABCD沿其对角线AC剪开,再把△ABC沿着AD方向平移,得到△A′B′C′,若两个三角形重叠的面积为S,则S与移动的距离AA′=x的函数关系式是y=-x2+12x(0≤x≤12);当x=6时,S有最大值36.
分析 作A′B′交AC于E,如图,AA′=x,根据正方形的性质得∠CAD=45°,AD=CD=12,再利用平移的性质得B′A′⊥AD,于是可判断△AA′E为等腰直角三角形,则A′E=AA′=x,利用平行四边形的面积公式得到
S=-x2+12x(0≤x≤12),然后根据二次函数的性质求S的最大值.
解答 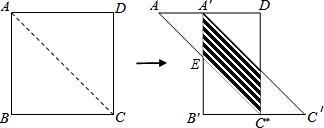 解:作A′B′交AC于E,如图,AA′=x,
解:作A′B′交AC于E,如图,AA′=x,
∵四边形ABCD为边长为12的正方形,
∴∠CAD=45°,AD=CD=12,
∵△ABC沿着AD方向平移,得到△A′B′C′,
∴B′A′⊥AD,
∴△AA′E为等腰直角三角形,
∴A′E=AA′=x,
∴S=A′E•A′D=x(12-x)=-x2+12x(0≤x≤12);
∵S=-(x-6)2+36,
∴当x=6时,S最大,最大值为36.
故答案为y=-x2+12x(0≤x≤12);6;36.
点评 本题考查了相似三角形的判定与性质,掌握平移的性质,会运用二次函数的性质解决有关最值问题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
15.如果把$\frac{5x}{x+y}$中的x与y都扩大为原来的10倍,那么这个代数式的值( )
| A. | 不变 | B. | 扩大为原来的5倍 | ||
| C. | 扩大为原来的10倍 | D. | 缩小为原来的$\frac{1}{2}$ |
17.计算2a3•a2的结果是( )
| A. | 2a | B. | 2a5 | C. | 2a6 | D. | 2a9 |

 如图表示一骑自行车好一骑摩托车者沿相同路线由甲地到乙地行驶过程中行驶时间与行驶路程变化的情况.已知甲,乙两地之间的距离是60千米,请你根据此图填空,并答题:
如图表示一骑自行车好一骑摩托车者沿相同路线由甲地到乙地行驶过程中行驶时间与行驶路程变化的情况.已知甲,乙两地之间的距离是60千米,请你根据此图填空,并答题:

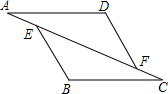 如图,已知:在△AFD和△CEB中,点A,E,F,C在同一条直线上,AE=CF,∠B=∠D,AD∥BC,请问:AD与BC相等吗?为什么?
如图,已知:在△AFD和△CEB中,点A,E,F,C在同一条直线上,AE=CF,∠B=∠D,AD∥BC,请问:AD与BC相等吗?为什么?