Question

16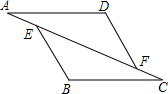．如图，已知：在△AFD和△CEB中，点A，E，F，C在同一条直线上，AE=CF，∠B=∠D，AD∥BC，请问：AD与BC相等吗？为什么？

Answer 1

分析 先求出AF=CE，再由平行线的性质得出∠A=∠C，由AAS证明△ADF≌△CBE，得出对应边相等即可．

解答 解：AD=BC，理由如下：
∵AE=CF，
∴AF=CE，
∵AD∥BC，
∴∠A=∠C，
在△ADF和△CBE中，$\left\{\begin{array}{l}{∠A=∠C}&{\;}\\{∠D=∠B}&{\;}\\{AF=CE}&{\;}\end{array}\right.$，
∴△ADF≌△CBE（AAS），
∴AD=BC．

点评 本题考查了平行线的性质、全等三角形的判定与性质；熟练掌握全等三角形的判定方法，证明三角形全等是解决问题的关键．